Investire per obiettivi significa spostare il focus dalla massimizzazione del rendimento alla massimizzazione delle probabilità di raggiungimento degli obiettivi (Goal Based Investing appunto, ossia investimento basato sugli obiettivi).
Prima di entrare nel merito, vediamo la storia che ha portato alla teorizzazione di questo modello.
Investire per obiettivi: la storia
E’ il 1952 quando Harry Markowitz pubblica il suo articolo Portfolio Selection, stravolgendo di fatto il modo nel quale tutti gli investitori, ma principalmente quelli istituzionali, avevano guardato fino a quel momento agli investimenti.
Come possiamo leggere dalla biografia di Jesse Livermore Reminescenes of a Stock Operator ma anche dal ben più noto libro L’investitore intelligente di Graham, in passato l’idea di investimento era quella di trovare uno o più asset performanti. Non veniva menzionato in nessun testo di considerare come quegli asset avrebbero interagito tra loro, men che meno esisteva l’idea di correlazione. Un portafoglio era un insieme di strumenti indipendenti tra loro.
In questo senso quella di Markowitz è una vera e propria rivoluzione. Fornisce un nuovo approccio basato sull’interazione tre le due variabili più iconiche negli anni a venire a tema investimenti: rendimento e rischio. Ma ancor di più, fornisce una definizione di rischio finanziario. Il rischio è la variabilità indefinita (o volatilità) degli investimenti. Si inizia quindi a percepire il rischio in una accezione molto più statistica, più materiale ma soprattutto misurabile rispetto a quanto fatto fino a quel momento.
Le critiche alla Modern Portfolio Theory e la nascita della Finanza comportamentale
Questo nuovo approccio, chiamato Modern Portfolio Theory, non è però esente da critiche, che riguardano principalmente le assunzioni alla base del modello. Una delle critiche più importanti riguarda il fatto che l’individuo è supposto come completamente razionale e il suo scopo è quello di minimizzare il rischio a parità di rendimento, rifuggendo sempre e comunque la volatilità ove possibile. La sua applicabilità è quindi indubbia per quanto riguarda la teoria e in parte anche per gli investitori istituzionali, ma il piccolo risparmiatore fatica a beneficiare di questo modello.
Una delle domande alla base delle critiche è: perché le persone acquistano sia l’assicurazione che i biglietti della lotteria?
Se è vero quindi che le persone sono sempre avverse al rischio in ogni circostanza, perché lo stesso individuo percepisce diversamente il rischio in base all’ambito? Perché l’individuo si tutela da alcuni rischi assicurandosi, ma al tempo stesso è disposto ad acquistare i biglietti della lotteria pur sapendo che le probabilità di vittoria sono infinitesimali?
Un tentativo di risposta lo abbiamo dagli stessi critici della teoria, Friedman e Savage, che ipotizzano che gli individui non abbiano solo una curva di utilità attesa ma N curve interconnesse tra loro.
Dobbiamo attendere però la fine degli anni ’80 per avere ulteriori risposte. Alcune di queste arrivano dalla finanza comportamentale, una nuova branca di studi che fa interagire economia e psicologia. Nello specifico dagli studi di Kahneman e Tversky. Ai quali poi si aggiunge Richard Thaler con il suo modello di mental accounting.
Quello del mental accounting, o contabilità mentale, è un approccio back to the future. Thaler nota come il tema centrale degli investitori privati sia la soddisfazione dei bisogni prima della massimizzazione del rendimento. Riprende quindi il concetto della Piramide dei bisogni di Maslow e arriva ad una conclusione semplice ma illuminante: le persone gestiscono i loro bisogni a compartimenti stagni. Ecco perché una persona acquista sia l’assicurazione che il biglietto della lotteria. Perché per alcuni aspetti necessita di sicurezza, mentre per altri è disposto a rischiare per arrivare a soddisfare i suoi bisogni.
La contabilità mentale è ciò che sta alla base del Goal Based Investing.
In cosa consiste investire per obiettivi
Il Goal Based Investing consiste in tre momenti principali:
- Analisi dei bisogni e definizione degli obiettivi
- Creazione dei portafogli per ciascun obiettivo
- Monitoraggio periodico
Il tutto presuppone ovviamente di aver analizzato in modo dettagliato l’attuale situazione finanziaria nella quale ci troviamo.
Analisi dei bisogni e definizione degli obiettivi
Questa fase è la più delicata ma anche la più snobbata, perché richiede una buona capacità di autoanalisi e obiettività, caratteristiche non comuni.
Ci viene però in aiuto la piramide dei bisogni finanziari. Un ottimo punto di partenza per analizzare i bisogni e definire gli obiettivi da raggiungere. I bisogni possono essere i più disparati, ma apparterranno sempre e comunque a due macrocategorie: bisogni di conservazione e bisogni di miglioramento.
Bisogni di conservazione
I primi si concretizzano nella necessità di non alterare negativamente la situazione finanziaria attuale.
Questi bisogni riguardano i livelli di protezione e liquidità.
In concreto, copertura assicurativa contro eventi potenzialmente catastrofici per le nostre finanze e per il nostro equilibrio familiare come assicurazioni per tutelarci in caso di premorienza o invalidità gravi di chi porta reddito in famiglia (fondamentale soprattutto in famiglia lavora solo una persona), assicurazioni sulla casa e per la responsabilità civile (il classico esempio del vaso che cade dal terrazzo e colpisce in testa un passante).
Tutte queste situazioni sono definite da Taleb come opzioni asimmetriche, dove il beneficio della non copertura è tendente a zero rispetto al danno potenziale derivante dal verificarsi dell’evento.
Per quanto riguarda invece la liquidità si traduce molto semplicemente nella creazione di un fondo di emergenza, ossia un capitale pari a (indicativamente) 6/9 volte le spese mensili familiari allo scopo di proteggere il nucleo familiare in caso di emergenze “reddituali” ossia emergenze che causano una riduzione temporanea dei nostri flussi di cassa o un aumento delle spese (ad esempio perdita del lavoro, automobile o elettrodomestici che si rompono e così via).
E’ importante ricordarsi che la caratteristica principale del fondo di emergenza non è quella di garantire un rendimento ma una protezione.
Bisogni di miglioramento
Risparmio, previdenza e investimento sono i tre bisogni finanziari che consentono di mantenere nel futuro la vostra attuale capacità di spesa e al tempo stesso vi danno la possibilità di migliorare la vostra condizione futura.
Il risparmio consente di traslare nel tempo la vostra ricchezza, ma da solo è insufficiente a mantenere inalterata la situazione attuale nel futuro a causa di un effetto ben noto che prende il nome di inflazione. L’euro risparmiato di oggi ha un potere d’acquisto minore di quello stesso euro domani.
Ecco che entra quindi in gioco la previdenza, ossia pensare alla pensione in tempo utile in modo da non ritrovarsi a 70 anni ed essere obbligati a lavorare per mantenere l’attuale stile di vita. La previdenza è un argomento talmente vasto che richiede un articolo dedicato.
Dobbiamo però considerare anche che la vita non è: nascere, studiare, lavorare, andare in pensione, morire. Nel mezzo ci sono migliaia di belle attività da poter fare che ci danno gioia.
Ad esempio, i figli sono uno dei motivi principali per i quali le persone investono. Quindi uno dei bisogno basilari di molti di noi è quello di mantenere un figlio e dargli tutto il nostro supporto affinché si realizzi. Inutile dire che per far questo servono soldi e per avere soldi occorre risparmiare e poi investire.
Poi ci sono anche bisogni forse meno nobili ma altrettanto validi: viaggiare, acquistare una casa, acquistare una barca, fondare la propria azienda e chi più ne ha più ne metta.
Ognuno di questi bisogni deve quindi essere tradotto in obiettivi.
Lo scopo di investire per obiettivi
Molto spesso vedo persone che dicono che il loro obiettivo è quello di fare più soldi. Questo non è un obiettivo. Fare più soldi non significa niente, ma peggio ancora questo presuppone che queste persone vedano il denaro come un fine e non come un mezzo. Questa logica è contraria a ciò che sta alla base dell’investire per obiettivi che vede il denaro come mezzo fungibile al raggiungimento di uno scopo.
Un obiettivo per essere definito tale deve essere S.M.A.R.T. :
- Specifico (Specific): una caratteristica importante è la chiarezza e la comunicabilità. Ad esempio: voglio comprare una casa non è un obiettivo specifico. Voglio comprare una casa di 80 mq in riva al mare in Sardegna è già più specifico;
- Misurabile (Measurable): un obiettivo presuppone il raggiungimento di un capitale certo. Se non sapete il controvalore della cosa alla quale puntate è un sogno, non un obiettivo;
- Raggiungibile (Achievable): tutti hanno dei sogni nel cassetto, ma dobbiamo fare i conti con la realtà. Una volta qualcuno ha detto che se punti alle stelle e va male almeno arrivi al cielo. Aggiungo che se va male davvero potresti anche schiantarti a terra;
- Realistico (Realistic): potrebbe sembrare un sinonimo del precedente ma la differenza è sostanziale. Voler lavorare come informatico in Google può essere un obiettivo raggiungibile, ma se avete 45 anni e lavorate come saldatore forse è un obiettivo poco realistico. Gli obiettivi raggiungibili ma non realistici sono quelli che presuppongono uno stravolgimento enorme delle vostre attuali condizioni in relazione alla vostra esperienza;
- Definito (e definibile) nel tempo (Time-bound): è necessario poter imporre una deadline al nostro obiettivo. La durata è una caratteristica fondamentale per una corretta pianificazione, perché la definizione del portafoglio dedicato a quell’obiettivo è fatta anche in funzione di questa variabile.
Aggiungo poi un sesto punto.
- Importanza: tanto più un obiettivo è essenziale da raggiungere tanto meno potete permettervi di rischiare per raggiungerlo. Di contro gli obiettivi non essenziali si definiscono ambiziosi.
Un esempio sul concetto di importanza.
Obiettivo: mi servono 30.000 euro tra 15 anni perché voglio mandare mio figlio a studiare in una Università prestigiosa. Capitale a scadenza: 30.000 euro. Durata: 15 anni. Importanza: essenziale.
Obiettivo: mi servono 30.000 euro tra 15 anni perché voglio comprarmi una barca. Capitale a scadenza: 30.000 euro. Durata: 15 anni. Importanza: ambizioso.
I due obiettivi hanno lo stesso capitale a scadenza e la stessa durata ma una diversa importanza, che si traduce in una maggior propensione al rischio del secondo obiettivo rispetto al primo. Questo significa, come vedremo più avanti, che posso destinare un capitale iniziale o periodico inferiore al secondo obiettivo ma investire in un portafoglio più rischioso.
Creazione dei portafogli per obiettivo
Arrivati a questo punto entra in gioco in concetto di contabilità mentale di Thaler. Una volta definiti gli obiettivi quindi dobbiamo considerare il capitale dedicato a ciascuno come contenitori distinti.
Questa strategia si pensava fosse subottimale rispetto a quanto stabilito dalla MPT, ma è stato dimostrato che non è così.
Avendo ben chiari i vostri obiettivi e per ciascuno di essi avendo ben chiare quali sono le variabili da considerare (capitale a scadenza, durata e importanza) dobbiamo procedere a definire il portafoglio per ciascun obiettivo.
In teoria sembra facile, nella pratica un po’ meno.
Questo perché il modello matematico alla base dell’investire per obiettivi presuppone ovviamente una ricchezza limitata. Non potete destinare ad un obiettivo più di quanto risparmiate in totale al netto di quanto destinate agli altri obiettivi.
Questo significa due cose: la prima è che dovete creare una classifica degli obiettivi, mentre la seconda è che il modello è ricorsivo.
La ricorsività del modello riguarda infatti la probabilità di raggiungere un obiettivo, che è funzione della ricchezza allocata (capitale iniziale e versamenti periodici) per quell’obiettivo e dell’asset allocation di quel portafoglio. Ma l’asset allocation dipende a sua volta dalla ricchezza allocata per quell’obiettivo.
Nota: una soluzione alla ricorsività può essere quella di impostare una asset allocation per livelli discreti di allocazione della ricchezza per poi trovare la massima utilità tramite l’applicazione di un modello Monte Carlo.
Lo scopo dei singoli portafogli non è quello di massimizzare il rendimento, ma di ridurre la probabilità di fallimento. E del calcolo della probabilità di fallimento ne ho già parlato in questo articolo.
Per ogni portafoglio quindi sarà importante definire il rendimento necessario al raggiungimento dell’obiettivo, rendimento atteso e volatilità (derivanti dall’analisi dei potenziali portafogli scelti). Con queste tre variabili e dato un intervallo di confidenza predeterminato possiamo calcolare Shortfall Risk e Safety-First Ratio al fine di trovare quali sono le combinazioni di portafogli migliori che ci consentono di raggiungere gli obiettivi, partendo da quelli essenziali e finendo a quelli maggiormente ambiziosi.
Una ulteriore complicazione del modello riguarda inflazione e tassazione. Quando stabiliamo un obiettivo è determinante considerare la tassazione sul capital gain che è una variabile nota ma è altrettanto importante fare delle ipotesi di andamento dell’inflazione futura, in particolar modo se l’orizzonte temporale è di lungo o lunghissimo termine. Anche in questo caso un modello Monte Carlo ci può venire in aiuto.
Monitoraggio periodico dell’investimento per obiettivi
Investire per obiettivi richiede un monitoraggio periodico in quanto gli obiettivi cambiano periodicamente. Su questa periodicità di scelta si basa la Life-Cycle Theory di Modigliani e Brumberg.
Gli studiosi hanno identificato quattro macrofasi nella vita di ognuno di noi, caratterizzate da una capacità reddituale e delle esigenze di spesa molto diverse tra loro.
La prima fase, che arriva intorno ai 25 anni, è identificata da capacità reddituale e di risparmio limitata, spesso negativa. Nella seconda fase, fino ai 40 anni circa, reddito e spesa crescono, ma nasce la necessità di far fronte ad alcuni eventi finanziariamente impattanti, come acquisto della prima casa, figli, automobile e così via. La terza fase, che arriva fino a 65 anni circa, è invece caratterizzata da una crescita dei redditi ridotta rispetto alla seconda fase, una stabilizzazione della spesa e quindi un incremento del risparmio. In questa fase è di fondamentale importanza pensare al futuro, ma continuando a sostenere economicamente i figli, non ancora autonomi. L’ultima fase è quella della pensione. La capacità reddituale si azzera, ma solitamente anche i consumi calano. In questa fase utilizziamo quanto accantonato nelle due fasi precedenti per mantenere il più possibile il nostro stile di vita.
Tutto questo si coniuga in un cambiamento costante dei nostri obiettivi, che devono essere monitorati periodicamente.
A questo si aggiunge anche un monitoraggio legato all’andamento dei portafogli. Questo monitoraggio consiste nell’aggiustare la rotta mano a mano che ci avviciniamo alla scadenza. Per esempio abbiamo impostato un obiettivo di 50.000 euro in 20 anni. Mancano 3 anni al termine ma i mercati sono andati particolarmente bene e abbiamo già superato il target. E’ importante quindi fare una riflessione sull’asset allocation di quel portafoglio, magari destinandolo interamente ad attività prive di rischio in ottica di conservazione del capitale per gli ultimi 3 anni.
Goal-Based Investing: dall’obiettivo al portafoglio
Step 1: definire gli obiettivi di investimento
Il primo step del Goal-Based Investing è ovviamente quello di aver ben chiari gli obiettivi e su questo vi posso aiutare ben poco. Come abbiamo già visto nell’articolo sulla pianificazione, ci sono diverse classificazioni degli obiettivi chiaramente visibili dalla Piramide dei Bisogni Finanziari. La definizione di tali obiettivi però spetta solo e soltanto a voi. Se per alcuni obiettivi come Sicurezza e Risparmio esistono linee guida universalmente applicabili, quelli relativi al quarto e quinto livello, cioè Previdenza e Investimento, richiedono analisi più approfondite.
Per quanto riguarda la previdenza è necessario definirne l’entità perché è un bisogno che ciascuno di noi ha. Ma per quanto riguarda la parte investimenti non solo è necessario definire numericamente i vari obiettivi, ma è fondamentale cercare di capire prima QUALI siano realmente i nostri obiettivi da perseguire. Far studiare i figli nelle migliori università, acquistare una nuova casa, comprare una barca, avviare un business, cambiare auto. C’è un ventaglio infinito di possibilità, ma la loro definizione è il primo passo fondamentale se vogliamo parlare di Goal-Based Investing. Se non avete chiari gli obiettivi da raggiungere tutto il castello cade e ci muoviamo a braccio, senza una direzione ben precisa.
Step 2: quantificare gli obiettivi
Una volta definiti gli obiettivi dobbiamo quantificarli.
Come ho scritto in un altro articolo dedicato al Goal-Based Investing, un obiettivo deve essere SMART, ossia specifico, misurabile, raggiungibile, realistico e definito. In aggiunta abbiamo parlato anche di importanza degli obiettivi. Questo significa che per ogni obiettivo dovrò avere ben chiari tre parametri fondamentali:
- capitale a scadenza
- durata
- importanza
Un esempio di obiettivo SMART è il seguente: voglio avviare un nuovo business tra 15 anni. Ho redatto un business plan e ho stimato i costi di avviamento che sono di circa 200.000 euro. E’ un obiettivo importante ma non essenziale in quanto ho già un lavoro ma vorrei mettermi in proprio per soddisfazione personale.
Quantificare un obiettivo prevede quindi non soltanto una conoscenza di se stessi, ma anche la capacità di stimare il capitale necessario in modo realistico. Questo non solo vi aiuta nella definizione dell’obiettivo, ma lo rende più reale, tangibile e, come piace tanto dire ai manager, traguardabile.
Non dobbiamo però dimenticarci di due aspetti fondamentali riguardo la quantificazione: inflazione e tassazione sulle plusvalenze.
Considerare l’inflazione
Tanto più l’obiettivo è lontano nel tempo, tanto più tenere in considerazione la svalutazione del potere d’acquisto risulta determinante.
Se ipotizzassimo una inflazione media nei prossimi 15 anni del 2%, il nostro obiettivo di 200.000 euro diventerebbe 270.000 euro. Una differenza del 35%. Non proprio qualcosa di trascurabile. Il calcolo è piuttosto semplice:
Capitale adeguato all’inflazione = capitale (1 + inflazione media stimata)numero di anni
Mi rendo conto che questa è una stima a spanne, in quanto l’inflazione non è costante nel tempo. Una inflazione maggiore nei primi anni e inferiore negli ultimi ci danneggerà meno rispetto al caso opposto, tuttavia credo che in questi casi una stima fatta a spanne porti ad un risultato migliore di una non stima.
Includere la tassazione
Includere la tassazione può essere più complesso rispetto a stimare il capitale rivalutato dell’inflazione, ma è un processo più preciso in quanto la tassazione è nota (a meno di cambiamenti normativi).
Calcolare l’impatto della tassazione sulle plusvalenze dipende da tre fattori:
- capitale a scadenza
- versato totale
- tassazione degli strumenti in portafoglio
Il terzo parametro è noto a prescindere. Per gli altri due dipende dal tipo di stima che vogliamo fare.
Step 3: definire una serie di portafogli ottimizzati
Impostato l’obiettivo del nostro modello di Goal-Based Investing occorre definire gli strumenti che si prestano meglio al raggiungimento dello stesso. In parole povere devo definire quali possono essere dei portafogli da utilizzare per massimizzare le probabilità di successo.
In questa fase è ancora presto per parlare di probabilità quindi mi limito semplicemente a definire quali possono essere una serie di portafogli ottimizzati da valutare. Se non avete alcuna esperienza di ottimizzazione di portafoglio il mio consiglio è di affidarvi ai grandi classici. Nel mio esempio infatti prenderò 4 portafogli molto diversi tra loro per profilo di rischio:
- Portafoglio 1: VWCE & Chill. Classico meme del subreddit ItaliaPersonalFinance. Un investimento 100% azionario in un unico ETF che replica l’andamento dell’indice FTSE All-World;
- Portafoglio 2: 60/40. Classicone. Costruito come combinazione tra VWCE e XGLE, ETF obbligazionario governativo con duration intorno ai 7 anni;
- Portafoglio 3: Permanent Portfolio. Ne ho parlato in questo articolo;
- Portafoglio 4: Risk free Portfolio. 100% in strumenti privi di rischio (come benchmark ho usato XEON).
Come abbiamo visto nell’articolo sul backtesting e la minimizzazione del cherry-picking, è buona norma prendere rendimenti e deviazione standard rollando scadenze dei portafogli per un orizzonte temporale pari alla durata residua del nostro obiettivo. Capisco che possa essere un esercizio non proprio facile, soprattutto se non abbiamo dimestichezza con linguaggi come python o R, ma ci permette di effettuare dei test più sensati rispetto a prendere un periodo storico unico.
Avendo fatto questo esercizio dal 2005 ad oggi sui 4 portafogli menzionati con ribilanciamento annuale, l’output è il seguente:
| Portfolio | Rendimento | Deviazione standard |
|---|---|---|
| VWCE (100% azionario) | 9,4% | 12,0% |
| 60/40 | 7,0% | 7,5% |
| Permanent Portfolio | 4,7% | 6,1% |
| Risk Free Portfolio | 1,0% | 0,0% |
Step 3: calcolare il rendimento minimo atteso
Una volta definito l’obiettivo, l’orizzonte temporale per raggiungerlo e un elenco di portafogli pseudo-ottimizzati (ho preso 4 lazy portfolio che più lazy non si può) possiamo iniziare il processo per definire qual è il portafoglio che, sulla carta, mi fornisce la probabilità maggiore di raggiungimento dell’obiettivo. Questo è un punto cardine del Goal-Based Investing.
Per effettuare questo calcolo è necessario avere già chiaro in mente il capitale iniziale da destinare all’obiettivo e/o l’entità dei versamenti periodici.
Supponendo di prendere come esempio l’obiettivo di 200.000 euro entro 15 anni, potrei volerlo raggiungere versando 20.000 euro in lump sum e 10.000 euro annualmente. Supponiamo inflazione e tassazione nulle per non appesantire il calcolo.
Applicando la formula excel del tasso di interesse (RATE) posso calcolare facilmente il rendimento minimo necessario per raggiungere l’obiettivo per i parametri ipotizzati, che è del 2,01% medio annuo per i 15 anni di durata dell’investimento.


Step 4: calcolare l’SFRatio e la probabilità di successo
Per ogni portafoglio posso calcolare il Roy’s Safety-First Criterion (SFRatio) utilizzando la formula
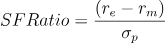
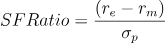
re = rendimento atteso del portafoglio
rm = rendimento minimo necessario
σp = deviazione standard del portafoglio| Portfolio | Rendimento | Deviazione standard | SF Ratio |
|---|---|---|---|
| VWCE (100% azionario) | 9,4% | 12,0% | 0,62 |
| 60/40 | 7,0% | 7,5% | 0,67 |
| Permanent Portfolio | 4,7% | 6,1% | 0,44 |
| Risk Free Portfolio | 1,0% | 0,0% | N/A |
Dato che il portafoglio risk-free ha una volatilità nulla non è possibile calcolare il Roy’s Safety-First Criterion. Questo non è un problema in quanto è comunque possibile calcolare la probabilità di raggiungimento dell’obiettivo che sarà 100% solo nel caso in cui il rendimento minimo atteso sia inferiore al rendimento atteso del portafoglio, 0% altrimenti. Logicamente questo ha senso in quanto se il mio rendimento atteso non si discosta mai dalla sua media durante il periodo so per certo che avrò 1% di rendimento per ogni anno dell’investimento.
Una volta calcolato l’SFRatio possiamo procedere a calcolare la probabilità di successo del portafoglio utilizzando la formula excel (o di google sheets) NORM.S.DIST (DISTRIB.NORM.ST.N in italiano) con parametro cumulata a TRUE. Questa formula consente di calcolare la probabilità cumulata che i miei rendimenti attesi ad una certa deviazione standard siano superiori alla fine del periodo al rendimento minimo necessario precedentemente calcolato.
Probabilità di successo = NORM.S.DIST(SFRatio*SQRT(Scadenza);1)


Il portafoglio che consente di massimizzare la probabilità di successo è il 60/40. Facendo un confronto col suo diretto concorrente, il 100% azionario, vediamo come la distribuzione dei rendimenti del portafoglio 60/40 tende a schiacciarsi maggiormente verso la media, anche se inferiore rispetto a quella di VWCE. La probabilità di successo non è altro che la probabilità che al termine del periodo la media dei rendimenti annuali sia maggiore del 2,01% (linea rossa).
Lo scopo infatti non è quello di massimizzare il rendimento, ma è quello di massimizzare le probabilità di raggiungere l’obiettivo. In parole povere, non voglio rischiare più di quanto mi serve per poter raggiungere l’obiettivo.
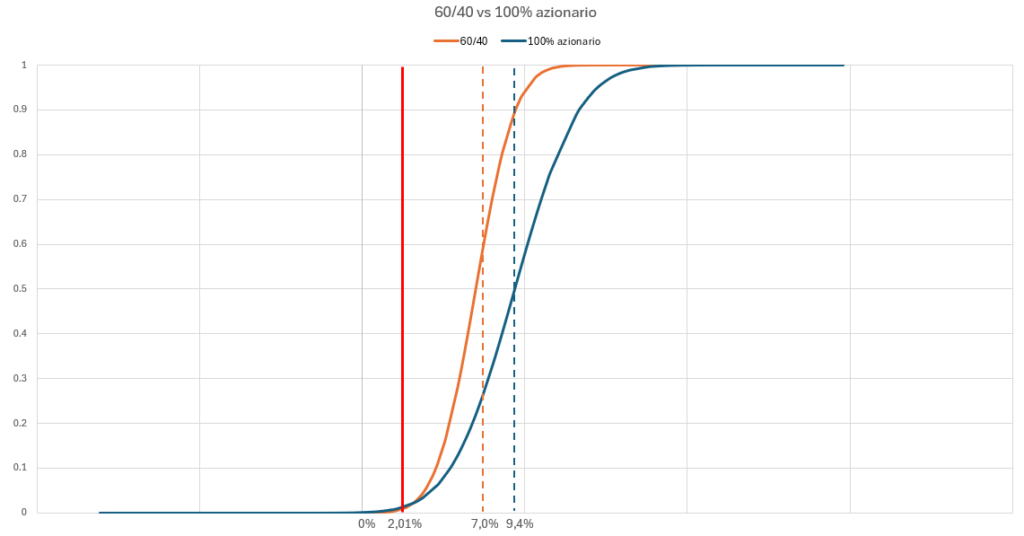

Per esempio, se impostassi una durata di 13 anni invece che di 15, la probabilità di successo sarebbe maggiore nel caso del portafoglio 100% azionario, in quanto il rendimento minimo necessario aumenterebbe dal 2,01% al 4,03%.


Viceversa, se allungassi la durata a 17 anni, il mio rendimento minimo atteso calerebbe allo 0,57% perciò il portafoglio migliore per raggiungere il mio obiettivo sarebbe il Risk-Free portfolio.


Moltiplicando il l’SFRatio per la radice quadrata della scadenza, tanto più il portafoglio ha una scadenza residua lunga tanto più la probabilità di successo è elevata. Tanto più ci avviciniamo alla scadenza, tanto più l’impatto del modello diventa utile.


Un approccio inverso di Goal-Based Investing
Fino ad ora ho ipotizzato che tra le variabili note ci sia il capitale iniziale ed eventuali versamenti aggiuntivi periodici. Tuttavia con lo stesso metodo posso calcolare quanto dovrei versare periodicamente dato un capitale iniziale.
Questo tipo di calcolo tuttavia presuppone una probabilità di successo scelta a priori. Solitamente le probabilità più note/utilizzate sono 99%, 95% e 90%. Tramite la funzione di distribuzione normale cumulata inversa possiamo convertire la probabilità in numero di deviazioni standard rispetto alla media (possiamo quindi calcolare quello che viene definito z-score). La formula di calcolo applicabile su Excel o Google Sheets è NORM.S.INV (INV.NORM.S. in italiano). Se supponiamo una probabilità di successo del 99%, il nostro z-score è 2,3263. Questo significa che la media annuale dei rendimenti futuri avrà una probabilità del 99% di “cadere” a destra rispetto al rendimento minimo atteso calcolato come:


rm = rendimento minimo atteso
rp = rendimento portafoglio
σ = deviazione standard del portafoglio
a = durata dell'investimentoDefinito un obiettivo di 200.000 euro per 15 anni di durata, 10.000 euro di capitale iniziale e una probabilità di successo del 99%, il miglior portafoglio per il raggiungimento dell’obiettivo è il portafoglio 60/40. Il rendimento minimo atteso maggiore è del 2,56% e mi consente di raggiungere l’obiettivo in 15 anni versando 10.298 euro all’anno.


Se accettassi una probabilità di successo inferiore perché reputo l’obiettivo come auspicabile e non necessario, potrei permettermi di versare annualmente un importo inferiore (8.846 euro ogni anno) selezionando il portafoglio più “aggressivo”, ossia quello 100% azionario.


Non è tutto oro quel che luccica
Il modello di Goal-Based Investing appena visto non è ovviamente esente da problemi.
Il primo problema è che i rendimenti giornalieri non sono distribuiti normalmente.
Di seguito abbiamo l’analisi statistica sui rendimenti giornalieri, settimanali, mensili e annuali rolling per gli ultimi 10 anni su SWDA. Quello che salta all’occhio è che i rendimenti rolling da dato giornaliero fino a mensile hanno una curtosi ben sopra il 3 (si dice che sono distribuzione leptocurtiche) e una forte asimmetria sinistra (maggior presenza di eventi eccezionali negativi). Graficamente la distribuzione dei rendimenti ha quella che viene definita fat tail. Tradotto, esiste una probabilità elevata di eventi eccezionali (più negativi che positivi se l’asimmetria è sinistra) quindi la varianza non è un parametro affidabile per misurare lo scostamento dalla media. Dovremmo invece utilizzare la mediana e la distribuzione interquartile.
Se però ci spostiamo ai rendimenti rolling annuali vediamo come la distribuzione diventa platicurtica e l’asimmetria è meno marcata e più spostata verso destra, quindi verso eventi eccezionali positivi.
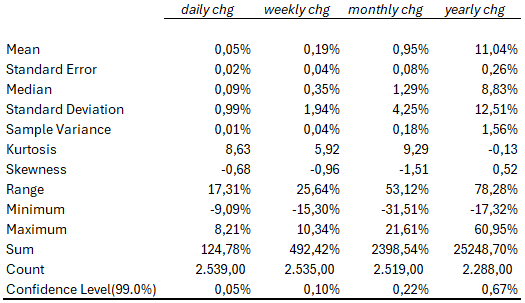

Il secondo problema, ben più impattante del primo, è che i rendimenti passati non sono indicativi dei rendimenti futuri. Se prendiamo una serie di portafogli ottimizzati calcolati su rendimenti storici, anche facendo attenzione a fare dei backtest affidabili ed evitare il cherry-picking, abbiamo comunque solo una vaga idea di quello che potrebbe accadere nei prossimi 10, 20 o 30 anni. Esistono modelli di ottimizzazione più avanzati rispetto al prendere la semplice media storica per intervalli temporali rolling, ma nessuno di questi ci può fornire con relativa certezza quale sarà la media dei rendimenti annuali futuri di un titolo.
Esiste comunque un fenomeno statistico definito regressione verso la media tale per cui tanto più un determinato titolo si discosta dalla sua media storica tanto più è probabile che in futuro tenderà a ritornare in media. Questo ci può dare qualche speranza in più, ma resta il fatto che stiamo brancolando nel buio con un fiammifero in mano. Possiamo solo scegliere se cominciare a correre a caso o se avanzare a tastoni. Io preferisco la seconda opzione.
Conclusioni
E’ impossibile esaurire l’argomento del Goal Based Investing in un solo articolo in quanto le tematiche da affrontare sono molte.
Se volete approfondire ulteriormente su Amazon trovate Goal-Based Wealth Management di Jean L.P. Brunel, in un certo senso il padre del Goal Based Investing, e Goal-Based Portfolio Theory di Franklin J. Parker. E ovviamente continuate a seguire il blog iscrivendovi alla newsletter tramite il link più in basso.
Grazie per la lettura.
Se questo articolo ti è stato utile, ecco alcuni modi per supportare il blog (e migliorare le tue finanze):
Strumenti che uso e consiglio
- Scalable Capital – Un broker che uso personalmente. Regime dichiarativo, oltre 2.500 ETF senza commissioni di acquisto, perfetto per PAC automatici.
- Moneyfarm – Gestione patrimoniale automatizzata con sostituto d’imposta. Ideale se non vuoi sbatterti a gestire tutto da solo senza farti mangiare dai costi delle banche tradizionali.
- Hype – Conto corrente a zero spese con IBAN italiano. Usa il codice HELLOHYPER per ottenere fino a 25€ di bonus all’apertura.
Risparmia sulle bollette
- Switcho – Servizio gratuito per trovare automaticamente il miglior fornitore di luce e gas. Il cambio è automatico e senza interruzioni.
Continua a imparare
- Audible – Ascolta i migliori libri di finanza durante i tragitti. Prova gratuita o 0,99€ per 3 mesi.
- Kindle Unlimited – Accesso illimitato a migliaia di ebook, molti gratuiti o scontati. Primo mese gratis.
Questi sono link affiliati. Se decidi di provare questi servizi, il blog riceve una piccola commissione senza alcun costo aggiuntivo per te. Consiglio solo strumenti che uso personalmente o che ritengo validi. Non sei obbligato a usarli, ma se l’hai trovato utile questo articolo, è un modo per supportare il progetto e permettermi di continuare a creare contenuti gratuiti.
Se ti è piaciuto l’articolo, iscriviti per rimanere aggiornato
Niente spam, ti invierò solo un aggiornamento settimanale.
DISCLAIMER
Non sono un consulente finanziario, ma un investitore comune che condivide il proprio percorso. Questo articolo è a scopo educativo. Le performance passate non garantiscono rendimenti futuri. La tassazione, i costi e le performance possono differire dai dati storici. Valuta attentamente la tua situazione personale, tolleranza al rischio e obiettivi finanziari. Se hai dubbi, consulta un professionista qualificato.