Quanti di voi hanno mai provato a calcolare quanto otterrebbero da un investimento azionario (che ha un rendimento storico medio del 7%) dopo 20 o 30 anni?
Immagino la maggior parte. La mirabolante regola del 72 è un tentativo estremo di semplificazione di questo concetto. Possiamo calcolare quanti anni ci mettiamo a raddoppiare il capitale investito dividendo 72 per il rendimento medio atteso. Se prendiamo come riferimento il rendimento storico del mercato azionario statunitense del 7%, impiegheremmo 10 anni e 3 mesi (72/7) a raddoppiare l’investimento.
I rendimenti storici vengono anche utilizzati per il calcolo della deviazione standard, per il calcolo dell’indice di Sharpe, per il calcolo dello Shortfall Risk, per pianificare gli obiettivi e chi più ne ha più ne metta.
Possiamo quindi dire che tutto quello che abbiamo in mano per fare valutazioni il più possibile oggettive sulle nostre scelte di investimento si basa sulla storia. Anzi, si basa su una media dei rendimenti storici.
Quanto è prudente utilizzare i rendimenti storici per pianificare i nostri obiettivi?
I rendimenti storici dell’S&P 500
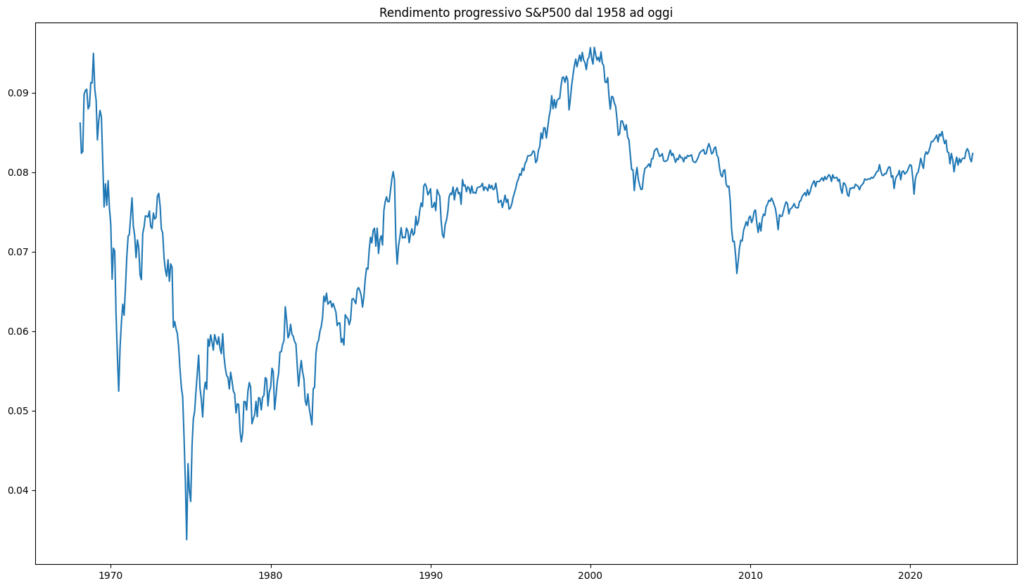
Guardiamo lo storico dello Standard & Poor 500 dal 1958 ad oggi e calcoliamo a progressivo la media dei rendimenti storici. Possiamo vedere come la media sia estremamente altalenante.
Se avessimo guardato ai rendimenti storici negli anni ’80 avremmo detto che il rendimento medio dell’S&P 500 è del 5%. Se lo avessimo guardato nel 2000, avremmo detto che il rendimento medio è del 9%. E’ una differenza enorme. Significa avere il doppio dei soldi dopo 20 anni.
Se lo guardiamo oggi, il rendimento medio dell’S&P500 è di circa l’8% dal 1958 ad oggi. Il problema è che non è detto che continuerà a rimanere su questo trend per i prossimi anni.

I rendimenti storici di un portafoglio diversificato
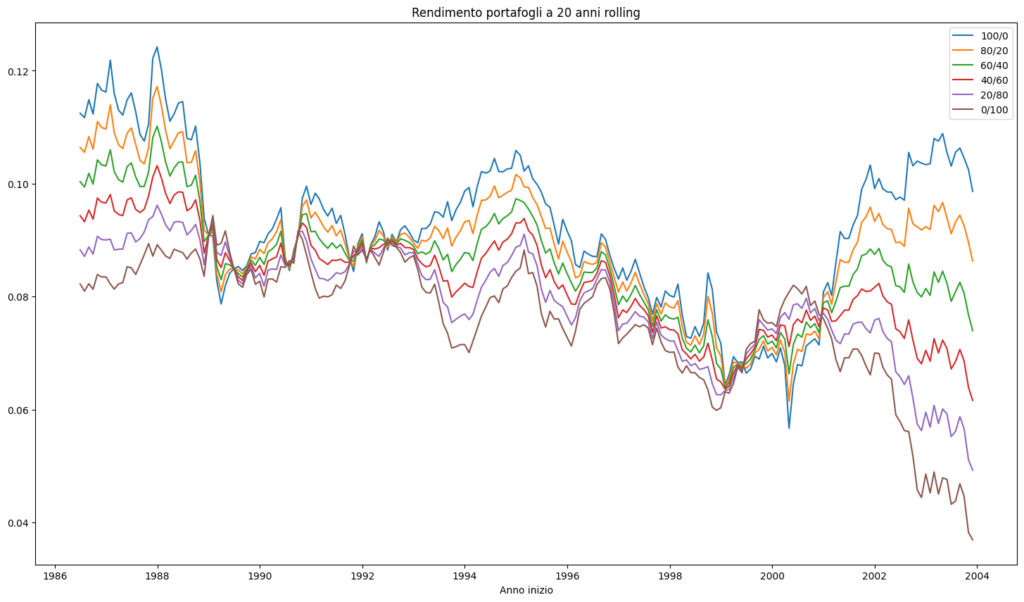
Possiamo quindi vedere come cambiano i rendimenti storici su base ventennale per una serie di portafogli (per avere una sufficiente base di storico ho preso solo il mercato statunitense), partendo dal 100% azionario e diminuendo progressivamente la quota del 20% a favore di un fondo obbligazionario governativo a lungo termine (duration a 20 anni circa).
Un portafoglio 100% azionario tenuto per 20 anni avrebbe generato un rendimento medio intorno all’11% se avessimo investito alla fine degli anni ’80, ma avrebbe generato un rendimento del 6-7% se avessimo investito intorno agli anni 2000.
Interessante vedere come se la scadenza coincide con una crisi di mercato i rendimenti dei vari portafogli convergono, mentre se siamo in un periodo di espansione i rendimenti divergono.
Il momento con maggiore divergenza è quello attuale, ma è dovuto ovviamente dalla crisi del mercato obbligazionario. E’ palese vedendo il crollo dei rendimenti delle obbligazioni a lungo termine (linea marrone, portafoglio 100% obbligazionario).

Se avessimo fatto lo stesso esercizio di calcolo dei rendimenti medi annuali su portafogli ventennali su S&P500 avremmo avuto lo stesso risultato.
Una variabilità estrema: dal 4% medio per un investimento effettuato negli anni ’60 a 20 anni ad un rendimento medio del 14% per un investimento effettuato negli anni ’80 e terminato nel 2000.


Come decidere quali rendimenti storici utilizzare in fase di pianificazione
Pianificare i propri investimenti ipotizzando che i mercati si comportino come hanno fatto IN MEDIA negli scorsi 50 anni è pericoloso. Il rischio di non raggiungere gli obiettivi è concreto.
Per ridurre (sottolineo ridurre, non annullare) il rischio di non raggiungimento degli obiettivi, quello che faccio è di sottostimare il rendimento atteso rispetto allo storico.
Un metodo di calcolo alla pene di segugio (anche detto a cazzo di cane) può essere quello di “tagliare” un buon 20-30% dei rendimenti storici. Se i rendimenti passati sono stati del 7% per portafogli ventennali potreste ipotizzare un rendimento atteso del 5%. E’ un metodo molto approssimativo in quanto la variabilità dei rendimenti dipende molto dalla volatilità.
Se volete essere un attimo più sofisticati potete costruire un modello Monte Carlo semplificato.
Metodo Monte Carlo
Il metodo Monte Carlo è un metodo di campionamento casuale, il cui scopo è quello di fare delle stime partendo da simulazioni. Il metodo si basa su un algoritmo che genera un serie di numeri casuali non correlati tra loro. In questo modo è possibile esplorare tutto lo spazio dei parametri del fenomeno analizzato. In finanza viene applicato per simulare una serie di possibili scenari futuri partendo da informazioni note, solitamente storiche.
Ho parlato di modello Monte Carlo semplificato, in quanto esistono diverse varianti del metodo, alcune più semplici e altre più complesse. Il modello più semplice si basa sull’assunto che i rendimenti siano normalmente distribuiti.
In realtà abbiamo già visto nell’articolo sulla gestione del rischio come gli eventi di coda non possono essere considerati come eventi irrilevanti nel calcolo del rendimento di un titolo, quindi sarebbe più corretto applicare un modello di distribuzione a coda larga, ma questo complicherebbe eccessivamente il calcolo. Lo scopo non è certo quello di stimare con certezza i rendimenti futuri (cosa che neanche il miglior modello di analisi statistica del mondo riesce a fare), ma è quello di stimare con ragionevole certezza il raggiungimento o meno di un obiettivo.
Per creare un modello Monte Carlo basato su una distribuzione normale dei rendimenti è sufficiente Excel (o Google Sheets) e la formula INV.NORM (o NORM.INV nella versione italiana).
In alternativa potete usare Python. La libreria NumPy mette a disposizione la funzione di densità di probabilità della distribuzione normale (random.normal).
Per esempio, il risultato di una simulazione di 100 iterazioni per un portafoglio decennale con 10000 euro di partenza e 1200 euro di versamenti annuali utilizzando come benchmark rendimento e volatilità dell’indice MSCI World dal 1970 ad oggi è rappresentato nel seguente grafico.


Visto così, il grafico può avere poco senso. Ma se analizziamo il valore dei portafogli di output abbiamo che:
- La media del capitale a scadenza è 37.250 euro;
- La mediana è di 35.674 euro (ossia quel risultato tale per cui il 50% dei portafogli ha fatto meglio e il 50% ha fatto peggio);
- Il 25° percentile (ossia quel risultato tale per cui il 75% dei portafogli ha fatto meglio e il 25% ha fatto peggio) è di 28.530 euro.
Applicando lo stesso concetto ai rendimenti medi attesi, abbiamo il seguente risultato:
- il rendimento medio è del 7,8% e mediano è del 7,6%;
- il rendimento del 25° percentile è del 4,9%.
Ho mostrato il 25° percentile perché può essere sufficientemente conservativo. Se volete essere ancora più prudenti, potete spingervi al 10° percentile, ossia quel risultato tale per cui il 90% degli altri portafogli ha fatto meglio e solo il 10% ha fatto peggio.
Conclusioni
Questo è un esempio di come concetti statistici possono venirci in aiuto quando siamo in fase di pianificazione degli obiettivi.
L’importante è non affidarsi unicamente ai rendimenti storici. Ne ho parlato anche in un recente articolo su come evitare di cadere nel cherry picking, ossia quel fenomeno tale per cui scegliamo opportunamente i rendimenti storici migliori per avvalorare le nostre scelte di investimento.
Il rischio concreto nel quale possiamo incorrere è di trovarci in prossimità della scadenza ed accorgersi che siamo troppo lontani dall’obiettivo. Se riusciamo ad aggiustare il tiro quando abbiamo ancora tempo a sufficienza, l’interesse composto riesce a darci una mano.
Tuttavia, ipotizzare di avere un ritorno medio dagli investimenti prendendo come riferimento il 10% di casi positivi estremi (ad esempio ipotizzando un rendimento del 9%, 10%, 11% da un investimento azionario) non fa altro che mettervi in una condizione di svantaggio. Dobbiamo avere l’onestà intellettuale di non aspettarci miracoli dai nostri investimenti, ma di ragionare stando sempre con i piedi ben saldi a terra.
E’ molto più conveniente vedere il bicchiere mezzo vuoto per poi rimanere piacevolmente sorpresi. Un pizzico di pessimismo è vantaggioso quando guardiamo al futuro.
Grazie per la lettura.
Se questo articolo ti è stato utile, ecco alcuni modi per supportare il blog (e migliorare le tue finanze):
Strumenti che uso e consiglio
- Scalable Capital – Un broker che uso personalmente. Regime dichiarativo, oltre 2.500 ETF senza commissioni di acquisto, perfetto per PAC automatici.
- Moneyfarm – Gestione patrimoniale automatizzata con sostituto d’imposta. Ideale se non vuoi sbatterti a gestire tutto da solo senza farti mangiare dai costi delle banche tradizionali.
- Hype – Conto corrente a zero spese con IBAN italiano. Usa il codice HELLOHYPER per ottenere fino a 25€ di bonus all’apertura.
Risparmia sulle bollette
- Switcho – Servizio gratuito per trovare automaticamente il miglior fornitore di luce e gas. Il cambio è automatico e senza interruzioni.
Continua a imparare
- Audible – Ascolta i migliori libri di finanza durante i tragitti. Prova gratuita o 0,99€ per 3 mesi.
- Kindle Unlimited – Accesso illimitato a migliaia di ebook, molti gratuiti o scontati. Primo mese gratis.
Questi sono link affiliati. Se decidi di provare questi servizi, il blog riceve una piccola commissione senza alcun costo aggiuntivo per te. Consiglio solo strumenti che uso personalmente o che ritengo validi. Non sei obbligato a usarli, ma se l’hai trovato utile questo articolo, è un modo per supportare il progetto e permettermi di continuare a creare contenuti gratuiti.
Se ti è piaciuto l’articolo, iscriviti per rimanere aggiornato
Niente spam, ti invierò solo un aggiornamento settimanale.
DISCLAIMER
Non sono un consulente finanziario, ma un investitore comune che condivide il proprio percorso. Questo articolo è a scopo educativo. Le performance passate non garantiscono rendimenti futuri. La tassazione, i costi e le performance possono differire dai dati storici. Valuta attentamente la tua situazione personale, tolleranza al rischio e obiettivi finanziari. Se hai dubbi, consulta un professionista qualificato.