In molti articoli pubblicati fino ad oggi ho condiviso analisi di portafoglio o di singole asset class, ossia il calcolo del rendimento di un portafoglio o di un investimento unito al calcolo del rischio relativo espresso come varianza. Saper analizzare i propri investimenti è uno step importante perché consente di essere critici rispetto alle scelte fatte, tenendo sempre presente che essendo un’analisi a posteriori ci aiuta ma non ci fornisce indicazioni precise sul futuro.
Analizzare un portafoglio significa valutare le performance degli asset al suo interno (azioni, obbligazioni, investimenti immobiliari, liquidità, crypto e così via) con lo scopo di misurarne le performance e il rischio su base assoluta e relativa.
Partiamo quindi dal calcolo dei rendimenti di un investimento, poi passeremo nei prossimi articoli ad analizzare il calcolo del rischio e infine faremo degli esempi di calcolo su portafogli reali.
Calcolo del rendimento semplice
Il calcolo del rendimento di un investimento significa calcolare la percentuale di variazione di un determinato investimento nel tempo. Tale variazione può essere positiva o negativa. Nel primo caso avremo generato un profitto, mentre nel secondo caso una perdita.
Il rendimento di un portafoglio è calcolato come segue:
Rendimento = [(Valore finale - Valore iniziale) + Dividendi] / Valore inizialeQuando calcoliamo il rendimento di strumenti ad accumulazione facciamo attenzione a selezionare i prezzi definiti come adjusted, ossia che includono i dividendi reinvestiti, in modo da semplificare il calcolo.
Calcolare il rendimento con questa formula, tuttavia, ha dei limiti.
Prendiamo per esempio due portafogli A e B. Entrambi hanno Valore iniziale = 10.000 € e supponiamo per semplicità che i dividendi siano 0 nel periodo di riferimento. Il portafoglio A ha un periodo di investimento di 10 anni ed un Valore finale di 20.000 € mentre il portafoglio B ha un periodo di investimento di 5 anni ed un Valore finale di 18.000 €.
Rendimento Portafoglio A = (20000 - 10000 ) / 10000 = 100%
Rendimento Portafoglio B = (18000 - 10000 ) / 10000 = 80%Ad una prima occhiata quindi il portafoglio A ha un rendimento maggiore del portafoglio B. Il problema è che non teniamo minimamente conto del fattore tempo, che è determinante per l’analisi di un portafoglio.
Calcolo del tasso medio di crescita annuale (CAGR)
Per tener conto del fattore tempo nel calcolo del rendimento di un investimento, dobbiamo calcolare quello che viene definito come Compound Annual Growth Rate (in breve CAGR), ossia il tasso di crescita medio annuale di un determinato portafoglio nel tempo.
CAGR = (Valore finale / Valore iniziale) ^ (1/N) - 1
N = numero di anni di investimentoRiprendendo l’esempio di poco ed applicando la formula del CAGR questi sono i risultati:
CAGR Portafoglio A = (20000 / 10000) ^ (1/10) -1 = 7,18%
CAGR Portafoglio B = (18000 / 10000) ^ (1/5) - 1 = 12,47%Diventa quindi chiaro come il portafoglio B ha un tasso di crescita annuale maggiore del portafoglio A, quindi nonostante abbia raggiunto un Valore finale minore è un portafoglio più redditizio rispetto al primo.
Anche la formula di calcolo del rendimento tramite CAGR, tuttavia, ha dei limiti. Tali limiti si riscontrano quando vogliamo calcolare il rendimento di un Piano di Accumulo Capitale (PAC) oppure quando facciamo conferimenti o riscatti dilazionati nel tempo.
Calcolo del rendimento di un PAC
Per esempio, introduciamo un portafoglio C gestito tramite PAC nel quale abbiamo un versamento iniziale di 5.000 € forfettario e i seguenti 5.000 € vengono investiti in soluzioni annuali di 1.000 € annui nei seguenti 5 anni. La durata dell’investimento è di 5 anni. Il Valore finale, avendo beneficiato meno dell’effetto di interesse composto, sarà di 15.000 €.
Applicando le formule viste precedentemente i risultati sono i seguenti:
Rendimento Portafoglio C = (15000 - 5000) / 5000 = 200%
CAGR Portafoglio C = (15000 / 5000) ^ / (1/5) - 1 = 24,57%Ad una prima occhiata, il rendimento del portafoglio C è enormemente più alto rispetto ai due precedenti. La realtà, tuttavia, è ben diversa, perché il Valore iniziale non tiene conto dei versamenti aggiuntivi fatti.
Per calcolare quindi il rendimento di un PAC ci aiutano il Time Weighted Rate of Return (TWRR) e il Money Weighted Rate of Return (MWRR).
Time Weighted Rate of Return (TWRR)
Il TWRR consente di calcolare il rendimento di un portafoglio suddividendo l’investimento in sottoperiodi. Ogni sottoperiodo è ciò che intercorre tra un conferimento (o un riscatto) e l’altro.
La formula di calcolo è la seguente:
Vn, ossia il valore del singolo sottoperiodo, è calcolato come segue:
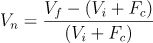
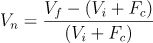
Vf = Valore finale del sottoperiodo
Vi = Valore iniziale del sottoperiodo
Fc = conferimenti o riscatti nel sottoperiodoMoney Weighted Rate of Return (MWRR)
Per calcolare correttamente il TWRR del PAC relativo al portafoglio C, dovremmo quindi conoscere l’andamento di tale portafoglio in ogni momento iniziale e finale rispetto ai singoli conferimenti di capitale. Tale metodologia non è di facile applicazione perché queste informazioni non sono sempre disponibili. Ecco quindi che possiamo applicare la formula di calcolo del MWRR.
La formula per il calcolo del MWRR è la seguente:
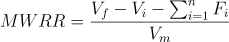
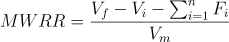
Vf = Valore Finale
Vi = Valore Iniziale
Fi = Flussi (conferimenti o riscatti durante il periodo)
Vm = Valore medio del periodoLa formula di calcolo della consistenza media è la seguente:
Tf = Data fine del periodo
tk = Data del conferimento/riscatto
Fk = conferimento/riscattoApplicando la formula di calcolo del Valore medio del periodo al portafoglio C otteniamo il seguente risultato:
Vm = 5000 + 4000/5 + 3000/5 + 2000/5 + 1000/5 = 7000A questo punto è possibile calcolare il MWRR, che sarà il seguente:
MWRR = 15000 - (5000 + 1000 + 1000 + 1000 + 1000 + 1000) / 7000 = 71,43%Di seguito il riepilogo del calcolo dei rendimenti dei 3 portafogli:
Rendimento semplice portafoglio A = 100%
Rendimento semplice portafoglio B = 80%
MWRR Portafoglio C = 71,43%Il rendimento del portafoglio C sul periodo di investimento risente del fatto che abbiamo investito in modo dilazionato quota parte del totale rispetto alle prime due soluzioni.
Una ulteriore informazione fornita dal confronto tra TWRR e MWRR è che:
- se MWRR > TWRR significa che le operazioni di conferimento e di riscatto intermedie ed il loro timing hanno migliorato la performance del portafoglio;
- se MWRR < TWRR significa che le operazioni di conferimento e di riscatto intermedie ed il loro timing hanno peggiorato le performance del portafoglio.
MWRR medio annuo
A questo punto, per confrontare il calcolo del rendimento di un investimento, potremmo avere necessità di confrontare i tassi medi annui di crescita per analizzare i 3 portafogli vincolandoli al fattore tempo.
Per far ciò abbiamo necessità di calcolare il MWRR medio annuo, il che significa risolvere la seguente equazione per l’incognita MWRR:
Per semplificare il lavoro, il magico Excel ci mette a disposizione una formula molto utile: XIRR() o TIR.X() se avete Office in italiano. La stessa formula è utilizzabile su Google Sheets nel medesimo modo.
Questa formula consente di calcolare il rendimento medio annuo per flussi di cassa positivi e negativi (investimenti e disinvestimenti) non costanti nel tempo.
Per farla funzionare dovete aver l’accortezza di trattare gli investimenti in segno negativo (uscite di denaro) e i disinvestimenti in segno positivo (come entrate) oppure viceversa. L’importante è fornire ad Excel dei flussi di cassa in entrambi i segni. Ovviamente stesso segno significa stesso tipo di operazione. Per esempio se ricevete dei dividendi periodici dai titoli detenuti potete conteggiarli nel calcolo del rendimento medio annuo inserendo in corrispondenza della relativa data di erogazione del dividendo l’importo in segno contrario agli eventuali versamenti effettuati sul portafoglio.
Calcolo del coefficiente Alfa
Un altro indicatore lato rendimenti che ci può tornare utile è il coefficiente Alfa, che calcola la differenza tra rendimento atteso e rendimento effettivo di un portafoglio.
Alfa = Tasso di rendimento effettivo di un portafoglio - Tasso di rendimento atteso di un portafoglioSe il coefficiente Alfa è positivo significa che il portafoglio oggetto di analisi ha avuto performance migliori di quelle attese, viceversa ha avuto un rendimento peggiore.
Tracking error
Il Tracking Error (o errore di tracciamento) è la differenza di rendimento tra un asset ed il suo benchmark. E’ particolarmente utile quando investiamo in strumenti poco liquidi per capire quanto si discosta quello strumento dal benchmark di riferimento oppure quando acquistiamo fondi a gestione attiva. Se il nostro portafoglio contiene solo strumenti a gestione passiva molto liquidi, il Tracking Error è minimo.
Tracking Error = Rendimento del portafoglio - Rendimento del benchmarkInformation Ratio
Nella gestione attiva di fondi di investimento, l’Information Ratio misura il rendimento per ogni unità di rischio aggiuntiva. Un Information Ratio maggiore di 1 significa che il gestore del fondo è stato in grado di generare un extra-rendimento rispetto al benchmark a parità di rischio, mentre un Information Ratio minore di 1 significa che il gestore ha generato un rendimento più basso rispetto al benchmark a parità di rischio (il che si può tradurre anche in stesso rendimento ma rischio minore nel primo caso oppure stesso rendimento e maggiore rischio nel secondo caso). E’ da preferire quindi un investimento che abbia un Information Ratio maggiore, in quanto significa che a parità di rischio quell’investimento ha generato storicamente un rendimento maggiore.
La formula di calcolo è la seguente:
Information Ratio = (Rendimento del portafoglio - Rendimento del benchmark) / Tracking ErrorConclusioni
Il calcolo del rendimento di un investimento è un passo fondamentale per l’analisi di un portafoglio ma non è l’unica analisi necessaria. L’altra variabile fondamentale per portare a termine un’analisi completa è il calcolo del rischio di un portafoglio, identificata dalla volatilità.
Grazie per la lettura.
Se ti è piaciuto l’articolo, iscriviti per rimanere aggiornato
Niente spam, ti invierò solo un aggiornamento settimanale.
Buongiorno,
inizio ringraziandoti per tutte le informazioni che riporti nel tuo blog/sito.
Mi sembra di aver capito che per l’investitore comune, che durante i mesi/anni sottopone il propio portafoglio a flussi di cassa (versamenti e prelievi) è di vitale importanza la funzione XIRR di excel per calcolare il rendimento annuo.
Fatta questa premessa, la mia domanda è: Esiste un altro metodo per fare questo calcolo? Chiedo perché la funzione XIRR necessita la presenza di una tabella con i vari flussi di cassa, questi nel corso degli anni tendenzialmente andranno ad aumentare, quindi mi ritroverei con una tabella dalle righe sempre più numerose. Esiste un modo più semplice che sommi il rendimento di un anno con quello dell’anno successivo o precedente?
Ciao, se non vuoi mantenere una tabella con i flussi di cassa puoi calcolare il CAGR per sottoperiodi (esempio per ogni anno), calcolando (valore finale/valore iniziale)^(1/anni)-1. Se lo calcoli per ogni anno ad esempio la formula è più semplice e diventa valore finale/valore iniziale -1.
Considera però che questa formula porta ad un risultato tanto meno preciso quanti più conferimenti e riscatti hai fatto durante l’anno.
Il grande vantaggio dell’MWRR sta proprio nel fatto di “depurare” il rendimento dall’effetto di flussi di cassa in ingresso e uscita effettuati con cadenze temporali diverse e spesso irregolari.
Considera comunque che non è necessario tenere una tabella dei flussi di cassa. Il tuo broker ti metterà a disposizione sicuramente nella schermata di Monitor Ordini la possibilità di estrarre via excel l’elenco dei flussi di cassa in entrata e uscita con relativa data. A quel punto è sufficiente aggiungere il valore attuale del portafoglio alla data di oggi con stesso segno dei disinvestimenti e calcolare l’MWRR annualizzato con la formula XIRR.
Ok, grazie per la tua risposta !