Microsoft Excel è tra gli strumenti aziendali più diffusi nelle aziende. Calcoli, grafici, analisi dei dati, modelli previsionali e così via. Per chi lavora nelle grandi banche di investimento o per gli analisti finanziari, Excel è uno strumento importante e conoscerlo sufficientemente può essere utile anche a noi, nonostante non sia richiesto di entrare eccessivamente in dettaglio di tutte le funzioni disponibili.
Ecco perché ho stilato un elenco di funzioni meno conosciute ma molto utili che possono supportarci nella pianificazione finanziaria. Non solo quindi per tutto ciò che riguarda gli investimenti, ma anche per rimborsare mutui, debiti e così via.
Considerate che tutte le funzioni che vedremo possono essere utilizzate anche su Google Sheets.
Stimare il valore futuro
Tramite la funzione Future Value FV() o VAL.FUT() per chi utilizza Excel in italiano è possibile stimare il valore futuro di un investimento o di un finanziamento con un tasso di interesse costante lungo tutta la durata e dei pagamenti periodici costanti.
Per esempio è possibile calcolare il valore futuro di un investimento di durata 20 anni con tasso del 6% annuale e versamento periodico di 1.200 euro annuale. Il risultato è 44.143 euro.
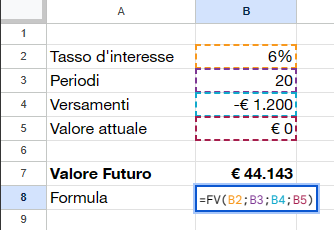
E’ possibile calcolare anche il valore futuro se i versamenti sono mensili. Per farlo dobbiamo impostare i valori da annuali a mensili.
Attualizzare un valore futuro
Se il nostro scopo è quello di attualizzare ad oggi il valore di un investimento futuro, possiamo utilizzare la funzione Present Value richiamabile con il comando PV() in inglese o VA() in italiano.
Tramite questa formula possiamo calcolare quanto è il valore che dovremmo investire oggi per ottenere un determinato capitale tra un determinato periodo ad un certo tasso di interesse.
Per esempio, se volessimo ottenere un capitale di 100.000 euro tra 20 anni ad un tasso medio annuale del 6% dovremmo investire oggi 31.180 euro.
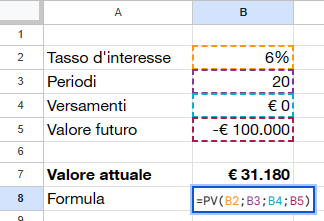
La stessa cosa è applicabile ipotizzando dei versamenti periodici per raggiungere l’obiettivo di 100.000 euro. In questo caso però dovremmo arrivarci “alla cieca”. Excel ci aiuta con una formula ben specifica: PMT.
Calcolo delle rate
La funzione PMT (o RATA() in italiano) è una delle mie preferite.
Consente di calcolare una rata per un finanziamento oppure il premio periodico di un investimento per ottenere un determinato capitale.
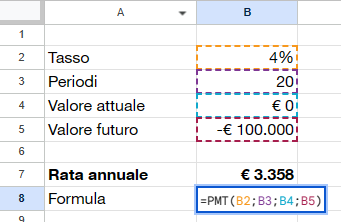
Per esempio se volessimo ottenere un capitale di 100.000 euro in 20 anni ad un tasso medio annuo del 4% partendo da zero, con la formula PMT() posso calcolare quale dovrebbe essere la rata annuale.
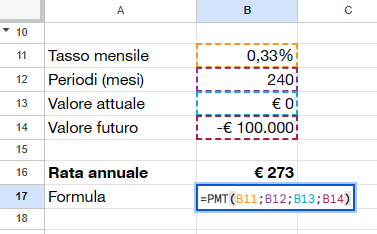
Posso anche convertire (lo vedete nella seconda immagine) in dati mensili e calcolare così una rata mensile che si discosta leggermente rispetto a quella annuale, dove gli interessi vengono pagati annualmente invece che mensilmente.
Questa funzione è molto utile sia per fare una stima per quanto riguarda un PAC sia per calcolare la rata di un eventuale mutuo o finanziamento a tasso fisso.
“La” formula dei rendimenti
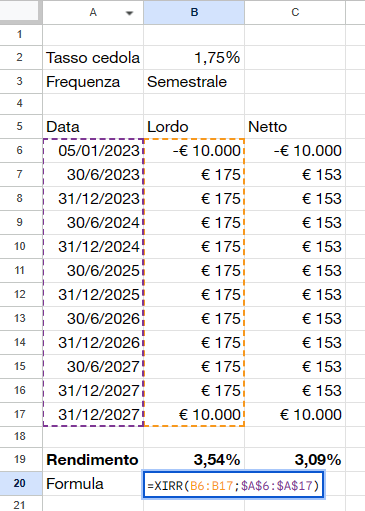
Sua maestà XIRR() o, in italiano, TIR.X(). E’ la formula Excel senza dubbio più utile per il calcolo dei rendimenti. Utilizzando questa formula non ve ne serviranno altre.
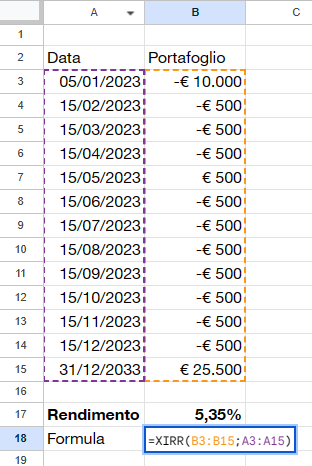
Consente di calcolare l’IRR, ossia il tasso interno di rendimento (TIR in italiano), partendo da dei flussi di cassa e relative date, anche non periodiche. E’ utilissima sia per il calcolo del rendimento lordo e netto di una obbligazione (sia essa a tasso fisso che a tasso variabile, sia step up, indicizzata e così via), sia per il calcolo del rendimento medio annuale di un portafoglio. E’ molto utile in particolar modo per il calcolo del rendimento di un portafoglio sul quale si fanno versamenti o disinvestimenti periodici e non (ad esempio un portafoglio alimentato tramite PAC oppure un portafoglio per generare una rendita passiva).
Quello che otterrete applicando questa formula è l’MWRR.
Se non sapete cosa è l’MWRR, potete leggere questo articolo.
Calcolo del tasso di interesse
Un’altra formula che utilizzo spesso insieme alla formula PMT() in fase di pianificazione degli obiettivi è la formula RATE() o, in italiano, TASSO().
Quando pianifichiamo un obiettivo conosciamo due variabili: capitale necessario a scadenza e durata temporale. Tutto ciò che sta nel mezzo è un’incognita. Se con la formula PMT() possiamo fare una stima, ipotizzando un tasso di interesse medio del portafoglio, di quanto dovrei versare periodicamente nel mio portafoglio, con la funzione RATE() posso stimare qual è il tasso minimo necessario per raggiungere il mio obiettivo.
Questo mi consente di aggiustare il tiro nel tempo, ma soprattutto mi dice se i miei piani sono realistici o meno. Se per arrivare all’obiettivo con l’attuale capacità di risparmio mi devo aspettare un tasso del 15% medio annuo è chiaro che quell’obiettivo diventa per me, al momento, irraggiungibile.
Questo però mi dice molto anche su quale tipo di portafoglio devo costruire per raggiungere quell’obiettivo, in quanto se il rendimento minimo necessario è del 3% posso sicuramente orientarmi su degli investimenti molto più conservativi e accollarmi un rischio minore. Questo mi consente di massimizzare le probabilità di raggiungimento del mio obiettivo, che è il rischio maggiore al quale dobbiamo stare attenti.
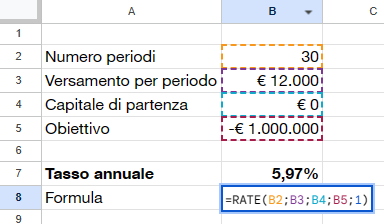
Quando utilizzate le formule PMT(), RATE(), FV() o PV() per calcolare le componenti di un investimento, è importante valorizzare il campo facoltativo della formula “fine o inizio” ad 1 (inizio). I versamenti a fini di investimento vengono effettuati all’inizio di un periodo, a differenza dei versamenti per finanziamenti/mutui che sono alla fine del periodo.
Nell’esempio seguente vediamo che per raggiungere 1 milione di euro in 30 anni versando 12.000 euro annui è necessario un rendimento medio annuo del 5,97%.
Calcolo del numero di versamenti
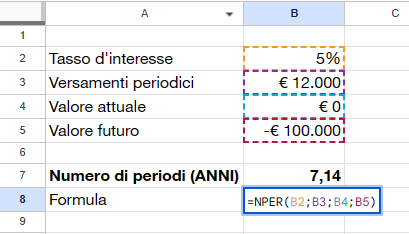
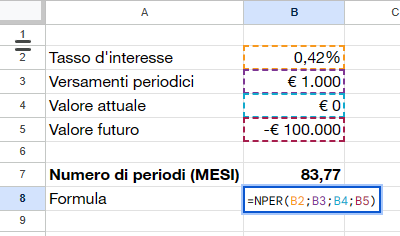
Se volete calcolare quanto tempo deve trascorrere affinché il vostro debito sia saldato o il vostro investimento arrivi all’obiettivo che vi siete prefissati ipotizzando un tasso di interesse medio e dei versamenti periodici costanti nel tempo, la formula NPER() o NUM.RATE() è quella che vi serve.
Nell’esempio ho ipotizzato di calcolare quanti anni servono per ripagare un debito di 100.000 euro versando 12000 euro annuali ad un tasso di interesse del 5%. La risposta è circa 7 anni.
Mensilizzando tasso di interesse e versamenti periodici possiamo anche stimare il numero di mesi che servono ad arrivare all’obiettivo. Fate molta attenzione quando utilizzate i valori mensili perché se il periodo è inferiore all’anno, vengono fatte delle assunzioni da Excel stesso che ipotizzano quel trend di andamento costante per tutto l’anno. Inoltre, fate attenzione a mensilizzare tutti i parametri: se impostate versamenti periodici a 1000 € ma interesse al 5% state stimando di ripagare un finanziamento per il quale versate 1000 euro al mese con un tasso MENSILE del 5%.
La formula della duration delle obbligazioni
La duration (o durata finanziaria) è una misura temporale che ci dice quanto impiega una obbligazione a ripagare, con le cedole, il capitale investito inizialmente. E’ una misura molto importante per stimare l’oscillazione del prezzo dell’obbligazione a seguito della variazione dei tassi di interesse.
Per fare un esempio calzante, ho selezionato un BTP dal sito web simpletoolsforinvestors.eu. Ho scelto il BTP 01/11/2033 4,35% (ISIN IT0005544082).
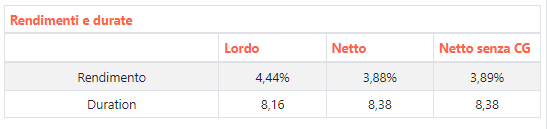
Ad oggi questo è il box del rendimento e della duration messo a disposizione direttamente dal tool.
Per calcolare la duration possiamo utilizzare la formula DURATION() o, se avete Excel in italiano, DURATA().
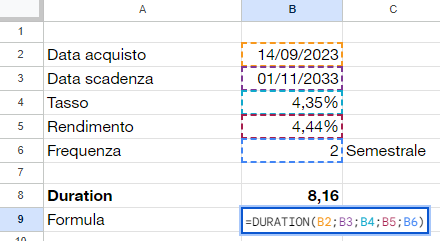
Selezionando la data di acquisto ad oggi, la scadenza del titolo, il tasso delle cedole del 4,35%, il tasso lordo calcolato dal tool e la frequenza di pagamento delle cedole (1=annuale, 2=semestrale, 4=trimestrale) abbiamo calcolato una duration perfettamente in linea con quella messa a disposizione da simpletoolsforinvestors.
Per capire come si muove l’obbligazione a seguito della variazione dei tassi di interesse dobbiamo però calcolare la duration modificata.
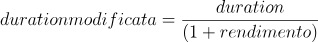
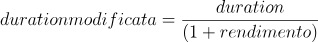
Nel nostro caso quindi a fronte di una duration di 8,16 e un rendimento del 4,44%, la duration modificata della nostra obbligazione è 7,81. Questo significa che una variazione dei tassi in aumento dell’1% comporta una diminuzione di prezzo del bond del 7,81%. Viceversa una diminuzione dei tassi comporterà un incremento del 7,81%.
Dato che ad oggi il prezzo del BTP sul mercato secondario è di 99,62 significa che un aumento dei tassi di un punto percentuale comporterebbe una riduzione del prezzo dell’obbligazione a 99,62 – 99,62 * 7,81% = 91,84
Il vantaggio è che molti tool online ma anche lo stesso sito di Borsa Italiana mettono a disposizione il dato già calcolato, senza bisogno di ricorrere a questa formula. E’ interessante però sapere il rapporto matematico tra durata e duration, in quanto ci consente di capire come la sensibilità di un titolo alla variazione dei tassi non dipenda soltanto dalla sua durata anche da quante cedole paga e da quanto è il suo prezzo attuale di scambio.
Un riepilogo delle formule Excel
| Obiettivo | Inglese | Italiano |
|---|---|---|
| Stimare il valore futuro di un investimento con un tasso costante e dei pagamenti periodici | FV() | VAL.FUT() |
| Attualizzare il valore di un investimento con tasso costante e pagamenti periodici | PV() | VA() |
| Calcolare il valore di una rata per il raggiungimento di un obiettivo | PMT() | RATA() |
| Calcolare il rendimento di un investimento con flussi di cassa non costanti | XIRR() | TIR.X() |
| Calcolare il tasso necessario per raggiungere un obiettivo | RATE() | TASSO() |
| Calcolare il numero di versamenti per arrivare all’obiettivo | NPER() | NUM.RATE() |
| Calcolo della duration di un titolo obbligazionario | DURATION() | DURATA() |
Conclusioni
Excel e Google Sheets sono due strumenti formidabili e i loro utilizzi sono vastissimi. Dovete solo fare attenzione a due aspetti: non fatevi spaventare dalle possibilità e, di contro, dato che potete non è detto che dobbiate farlo. Il secondo problema è più subdolo del primo. Molto spesso parlo con persone che genererebbero file excel anche per tracciare le entrate e le uscite di centesimi nei loro portafogli.
Manteniamola semplice, facciamoci aiutare dalla tecnologia ma senza esagerare.
Grazie per la lettura.
Se ti è piaciuto l’articolo, iscriviti per rimanere aggiornato
Niente spam, ti invierò solo un aggiornamento settimanale.
