Aggiornamento 2025: Questa guida avanzata approfondisce metodologie di analisi del rischio utilizzate da investitori istituzionali: Coefficiente Beta, Value at Risk (VaR) e Conditional Value at Risk (CVaR).
Se cerchi un’introduzione base al rischio degli investimenti, inizia dalla Parte 1: Deviazione Standard e Sharpe Ratio. Questo articolo è dedicato a chi vuole strumenti di analisi più sofisticati.
Cosa imparerai:
- Distinguere rischio sistematico e non sistematico
- Calcolare il Coefficiente Beta con Excel
- Misurare il rischio con Value at Risk (VaR)
- Analizzare il tail risk con CVaR
TL;DR – Metriche Avanzate Rischio
- Beta: Volatilità relativa al mercato (β<1 difensivo, β>1 aggressivo)
- VaR 95%: Perdita massima in 19 giorni su 20
- CVaR: Perdita media quando VaR viene superato (tail risk)
- Tool: Excel con formule COVARIANZA.P, PERCENTILE, PENDENZA
- Target: Investitori avanzati, analisi istituzionale
- Tempo lettura: 8 minuti
Rischio sistematico vs non sistematico: le differenze chiave
Il rischio sistematico è il rischio legato all’intero mercato ed è definito come imprevedibile e non diversificabile. L’unico metodo per contrastare questo tipo di rischio è fare ricorso all’hedging. Un esempio di rischio sistematico potrebbe essere il COVID. Essendo un evento imprevedibile che ha colpito trasversalmente tutti i mercati può rientrare nella classificazione di rischio sistematico (o instabilità sistematica).
Il rischio non sistematico è il rischio legato ad un singolo settore, ad una singola azienda e (alcuni forse potranno storcere il naso) ad un singolo paese. Se investo tutto il mio capitale su Microsoft e Microsoft fallisce, perdo tutto il mio capitale. Se investo tutto il mio capitale su bond rumeni e la Romania va in default, perdo tutto il mio capitale. Il rischio non sistematico è evitabile attraverso una corretta diversificazione.
Le metodologie di misurazione del rischio che stiamo analizzando hanno lo scopo di (provare a) misurare il rischio sistematico.
Coefficiente Beta: cos’è e come calcolarlo
Abbiamo visto nel primo articolo sulla misurazione del rischio come nella Modern Portfolio Theory rischio = volatilità = deviazione standard.
Il coefficiente Beta (β) è un coefficiente di misurazione della volatilità relativa. Il suo scopo è quello di rapportare la volatilità di un titolo o di un portafoglio al suo benchmark (il mercato di riferimento). Il beta potrà assumere valori maggiori, minori o uguali ad 1. Un β maggiore di 1 sta ad indicare che il titolo che stiamo analizzando ha una volatilità maggiore del benchmark. Un β minore 1 indica che il titolo ha una volatilità minore del benchmark. Un β uguale ad 1 significa che titolo e benchmark hanno stessa volatilità (ossia stesso rischio sistematico).
La formula di calcolo del β è la seguente:
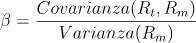
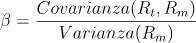
Rt = rendimento del singolo titolo
Rm = rendimento del benchmarkLa covarianza indica la variazione dei rendimenti del titolo in relazione alla variazione dei rendimenti del mercato di riferimento, mentre la varianza indica quanto i rendimenti differiscono rispetto alla media.
Come calcolare il Coefficiente Beta con Excel (2 metodi)
- Metodo 1: COVARIANCE.P ( rendimenti giornalieri azione ; rendimenti giornalieri benchmark ) / VAR.P( rendimenti giornalieri benchmark )
- Metodo 2: SLOPE (rendimenti giornalieri azione ; rendimenti giornalieri benchmark)
Esempio pratico: calcolare il Beta di un’azione
Supponiamo di voler calcolare il Beta di un’azione rispetto all’indice FTSE MIB.
Abbiamo raccolto i rendimenti giornalieri degli ultimi 252 giorni di trading (un anno).
Su Excel:
- Colonna A: Date
- Colonna B: Rendimenti azione
- Colonna C: Rendimenti FTSE MIB
- Cella E1:
=COVARIANZA.P(B:B;C:C)/VAR.P(C:C) - Oppure cella E2:
=PENDENZA(B:B;C:C)
Interpretazione risultati 2025:
- β = 0.8 → L’azione è meno volatile del mercato (difensiva)
- β = 1.0 → L’azione si muove con il mercato
- β = 1.5 → L’azione è più volatile del mercato (aggressiva)
Nel contesto di mercato volatile del 2025, titoli con beta basso (<1) tendono a
proteggere meglio il portafoglio durante le correzioni.
Vuoi vedere il Beta del tuo portafoglio?
[Scalable Capital](LINK_AFFILIATO) offre analisi avanzate del rischio incluse:
✅ Coefficiente Beta calcolato automaticamente
✅ Correlazione con indici di riferimento
✅ Analisi della volatilità del portafoglio
✅ Report rischio/rendimento professionale
⚡ Apertura in 10 minuti • ✅ Nessun deposito minimo obbligatorio • 💳 PAC su ETF gratis
Link affiliato – Ricevo una commissione senza costi aggiuntivi per te. Info sulla trasparenza
Value at Risk (VaR): misurare la massima perdita potenziale
All’interno del ventaglio delle possibilità su come misurare il rischio di un investimento, abbiamo il Value at Risk (VaR). E’ una misura statistica che serve a quantificare l’ammontare delle possibili perdite di un portafoglio o di un titolo. E’ definito come la massima perdita potenziale in un determinato periodo di tempo all’interno di un intervallo di confidenza (solitamente del 95% o del 99%).
Graficamente lo possiamo rappresentare come segue. Sull’asse delle ascisse abbiamo la deviazione standard, sulle ordinate il numero di misurazioni per livello di volatilità, in blu i rendimenti dell’S&P500 e la linea nera rappresenta la curva di Gauss.
Il VaR analizza la “coda” della campana di Gauss per un intervallo di confidenza (solitamente del 95% o del 99%) e per un intervallo temporale (solitamente un giorno o due settimane).
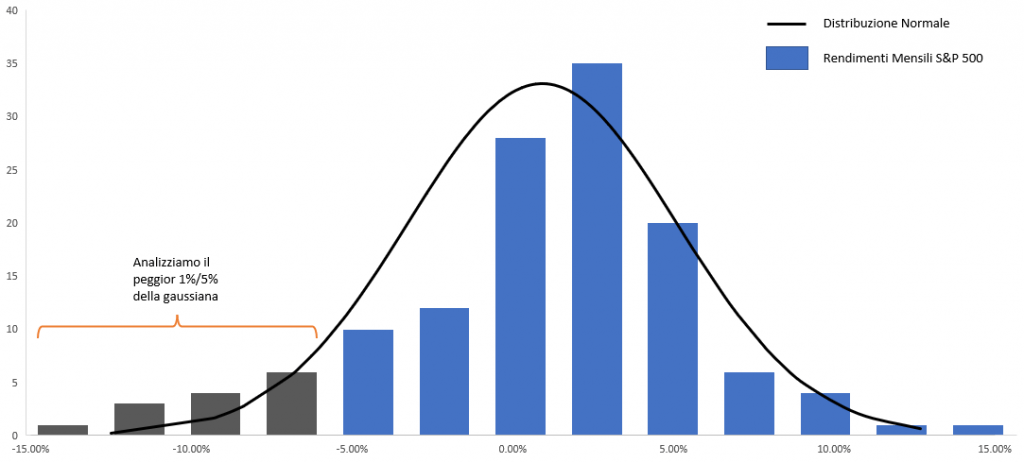

Quando parliamo di rischio di un investimento misurato tramite Value at Risk dobbiamo sempre far riferimento sia alla probabilità che tale evento si verifichi sia all’ammontare della perdita. Per esempio potremmo dire che un portafoglio ha un VaR giornaliero del 5% di 1.000 €. Significa che quotidianamente la probabilità di incorrere in una perdita di 1.000€ è del 5%.
Formula VaR e calcolo parametrico
Il calcolo del VaR può avvenire in 3 modi:
- Analisi delle serie storiche;
- Metodo della varianza – covarianza (detto anche parametrico);
- Metodo Montecarlo.
Guardiamo in dettaglio il metodo di calcolo parametrico, che avviene applicando la seguente formula.
VaR % = Numero di deviazioni standard in base all’intervallo di confidenza * σ * √T
Var € = valore del portafoglio * VaR %
T = numero di giorni per i quali vogliamo calcolare il VaR
σ = deviazione standardIl numero di deviazioni standard in base all’intervallo di confidenza è tabellato (o calcolabile tramite Excel):


Per calcolare il VaR giornaliero di un portafoglio di 100.000 € con intervallo di confidenza al 95% e deviazione standard del 1%, la formula da applicare è la seguente:
VaR % = 1,645 * 0,01 * √1 = 1,645%
VaR € = 100.000 * 1,645% = 1.645 €
La massima perdita potenziale per un intervallo di confidenza al 99% di un portafoglio del valore di 100.000 € con deviazione standard dell’1% è di 8.224 €.
Esempio pratico: calcolare VaR su Excel
Se avessimo voluto calcolarlo con orizzonte temporale mensile la formula sarebbe stata la seguente:
VaR % = 1,645 * 0,01 * √30 = 9,01%
VaR € = 100.000 * 9,01% = 9.010 €
Attenzione a non confondere il VaR con la perdita massima effettiva. Potenzialmente entro quel determinato intervallo di confidenza possiamo presumere che la nostra perdita sia quella indicata dal calcolo del Value at Risk, ma al di fuori di quell’intervallo di confidenza potremmo subire perdite più consistenti.
Ecco che ci viene in aiuto il CVaR.
Conditional Value at Risk (CVaR): analisi del tail risk 2025
Il CVaR, detto anche Expected Shortfall (ES), Expected Tail Loss (ETL) o Average Value at Risk (AVR), è la diretta evoluzione del Value at Risk. Il CVaR ha come scopo quello di calcolare l’effettiva perdita massima che un titolo o un portafoglio possono subire in un intervallo temporale oltre l’intervallo di competenza impostato per il calcolo del VaR.
Nel titolo del paragrafo abbiamo parlato del CVaR come metodo di misurazione dei tail risk (o tail loss). Il rischio di coda è la probabilità che un determinato titolo o portafoglio abbia rendimenti che si scostano dalla media di più di 3 deviazioni standard. Teoricamente, per una distribuzione normale, la probabilità che ciò accada è infinitesimale, ma è stato dimostrato nella pratica che tali eventi nei mercati finanziari si verificano con maggior frequenza.
Il calcolo del CVaR di genera come media ponderata delle perdite estreme nella coda della curva (oltre il breakeven del VaR) per la distribuzione dei rendimenti di un determinato titolo o portafoglio. Il CVaR sarà sempre maggiore o uguale al VaR.
Solitamente, per azioni large cap statunitensi oppure bond investment grade il CVaR non si discosta molto dal VaR. Discorso diverso invece può essere fatto per titoli di asset più volatili, come small cap, indici di mercati emergenti oppure per strumenti come i derivati. Gli investitori di lungo periodo tenderanno a preferire asset nei quali VaR e CVaR tendono ad essere più vicini tra loro, mentre operatori che hanno come scopo quello di beneficiare di rialzi importanti tenderanno a cercare strumenti che abbiano un CVaR più elevato.
VaR vs CVaR: quale scegliere nel 2025?
| Caratteristica | Value at Risk (VaR) | CVaR (Expected Shortfall) |
|---|---|---|
| Cosa misura | Perdita massima al X% | Perdita media oltre il VaR |
| Considera tail risk | ❌ No | ✅ Sì |
| Calcolo Excel | Medio | Complesso |
| Uso istituzionale | Standard pre-2008 | Standard post-2008 |
| Consigliato per | Portafogli diversificati | Portafogli concentrati |
| Best for 2025 | Analisi base | Analisi avanzata |
Consiglio 2025: Usa entrambi. VaR per screening rapido, CVaR per analisi approfondita del rischio di coda.
Gestione professionale del rischio con stress test avanzati
Moneyfarm applica metodologie istituzionali al tuo portafoglio:
✅ Analisi VaR e stress test regolari
✅ Monitoraggio rischio sistematico continuo
✅ Ribilanciamento automatico per controllo volatilità
✅ Reportistica professionale mensile
⚡ Analisi in 10 minuti • 🤝 Consulente dedicato • 📊 Portafogli diversificati
Link di affiliazione. Non ci sono costi aggiuntivi – Info sulla trasparenza
Domande frequenti su Beta, VaR e CVaR
Qual è la differenza tra rischio sistematico e non sistematico?
Il rischio sistematico riguarda l’intero mercato (es. recessione globale) ed è
non diversificabile. Il rischio non sistematico è specifico di un’azienda/settore
ed è eliminabile con la diversificazione.
Come si calcola il Coefficiente Beta?
Il Beta si calcola con: Beta = Covarianza(Rendimenti Azione, Rendimenti Mercato) /
Varianza(Rendimenti Mercato). Su Excel: =COVARIANZA.P(azione;mercato)/VAR.P(mercato)
o più semplicemente =PENDENZA(azione;mercato).
Cosa significa un VaR giornaliero del 5% di 1.000€?
Significa che c’è una probabilità del 5% (1 giorno su 20) di perdere almeno 1.000€
in un singolo giorno di trading.
CVaR è meglio del VaR?
Il CVaR è più conservativo perché misura la perdita media quando il VaR viene superato.
È preferibile per analisi tail risk e portafogli concentrati. Il VaR è più rapido
per screening iniziale.
Quale intervallo di confidenza usare per VaR?
- 95% per analisi standard e portafogli moderati
- 99% per portafogli aggressivi o analisi conservative
- 99.5% per requisiti istituzionali stress test
Conclusioni: quali metriche usare nel 2025
I coefficienti atti a misurare il rischio di un investimento sono i più disparati. Ho voluto illustrarvi alcuni dei principali, ma nell’operatività normale quello che serve a noi investitori comuni è gestibile con un file Excel ben strutturato.
Non fatevi impaurire da formule statistiche o concetti eccessivamente complessi. E’ giusto conoscere, perché in questo modo si riesce ad utilizzare tutto ciò di cui abbiamo bisogno, senza rimanere nella paura che esista un metodo di stima dei rendimenti o del rischio migliore di quello che stiamo applicando.
Grazie per la lettura.
Se questo articolo ti è stato utile, ecco alcuni modi per supportare il blog (e migliorare le tue finanze):
Strumenti che uso e consiglio
- Scalable Capital – Un broker che uso personalmente. Regime dichiarativo, oltre 2.500 ETF senza commissioni di acquisto, perfetto per PAC automatici.
- Moneyfarm – Gestione patrimoniale automatizzata con sostituto d’imposta. Ideale se non vuoi sbatterti a gestire tutto da solo senza farti mangiare dai costi delle banche tradizionali.
- Hype – Conto corrente a zero spese con IBAN italiano. Usa il codice HELLOHYPER per ottenere fino a 25€ di bonus all’apertura.
Risparmia sulle bollette
- Switcho – Servizio gratuito per trovare automaticamente il miglior fornitore di luce e gas. Il cambio è automatico e senza interruzioni.
Continua a imparare
- Audible – Ascolta i migliori libri di finanza durante i tragitti. Prova gratuita o 0,99€ per 3 mesi.
- Kindle Unlimited – Accesso illimitato a migliaia di ebook, molti gratuiti o scontati. Primo mese gratis.
Questi sono link affiliati. Se decidi di provare questi servizi, il blog riceve una piccola commissione senza alcun costo aggiuntivo per te. Consiglio solo strumenti che uso personalmente o che ritengo validi. Non sei obbligato a usarli, ma se l’hai trovato utile questo articolo, è un modo per supportare il progetto e permettermi di continuare a creare contenuti gratuiti.
Se ti è piaciuto l’articolo, iscriviti per rimanere aggiornato
Niente spam, ti invierò solo un aggiornamento settimanale.
DISCLAIMER
Non sono un consulente finanziario, ma un investitore comune che condivide il proprio percorso. Questo articolo è a scopo educativo. Le performance passate non garantiscono rendimenti futuri. La tassazione, i costi e le performance possono differire dai dati storici. Valuta attentamente la tua situazione personale, tolleranza al rischio e obiettivi finanziari. Se hai dubbi, consulta un professionista qualificato.