La moderna teoria del portafoglio (MPT) stabilisce che misurare il rischio di un investimento è possibile calcolando la volatilità degli asset che fanno parte del portafoglio. La visione di rischio inteso come volatilità non è l’unica modalità possibile di guardare al rischio, ma è sicuramente un metodo misurabile ed oggettivo ed è quello che analizzeremo in questo articolo.
Se ve lo siete perso, qua trovate il primo articolo sull’Analisi di Portafoglio, incentrato sul calcolo del rendimento.
La volatilità viene definita tramite la deviazione standard, ossia un asset è tanto più rischioso quanto più i valori sono lontani dalla media e tanto più un asset è definito come rischioso tanto più il rendimento atteso è maggiore.
Aggiornamento 2025: Con l’aumento della volatilità dei mercati negli ultimi anni, misurare correttamente il rischio del proprio portafoglio è diventato ancora più cruciale. In questa guida aggiornata, vedremo come calcolare la volatilità e il rischio del tuo portafoglio investimenti usando strumenti accessibili come Excel.
In sintesi
- Rischio = Volatilità: misurata con deviazione standard
- Formula Excel: DEV.ST.P() per calcolo immediato
- Indice di Sharpe: confronta rendimento vs rischio
- Analisi periodica: verifica annuale consigliata
- Tempo lettura: 10 minuti
Come misurare il rischio di un investimento nel 2025
Prima di entrare nei dettagli tecnici, è importante capire perché misurare il rischio del tuo portafoglio investimenti è fondamentale, soprattutto in un contesto di mercato incerto come quello che stiamo vivendo nel 2025.
Cos’è la deviazione standard per misurare il rischio investimenti
La deviazione standard è un indice di dispersione statistico che stima la variabilità di una popolazione. Con indice di dispersione si intende quanto i valori di una popolazione sono dispersi intorno alla loro media. E’ la variabile più diffusa per misurare il rischio di un investimento.
Di seguito un grafico di due portafogli con stessa media dei rendimenti (μ=5%) ma con deviazione standard diversa (σ al 3% nel portafoglio blu e σ al 10% nel portafoglio arancione).
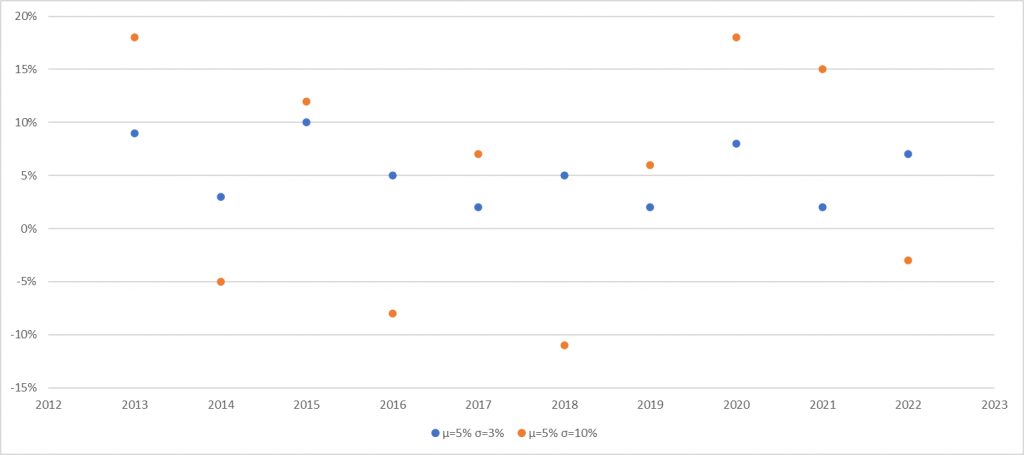

Si vede a colpo d’occhio cosa si intende per variabilità dei valori intorno alla media. Pur avendo lo stesso rendimento, i due portafogli hanno due deviazioni standard ben diverse. Questo è derivato dal fatto che i rendimenti del portafoglio blu tendono ad avere un scarto medio minore dal rendimento medio del 5% mentre quelli del portafoglio arancione tendono a distanziarsi maggiormente. Il portafoglio arancione quindi sarà considerato più rischioso del portafoglio blu.
Come calcolare la deviazione standard su Excel
La formula di calcolo della deviazione standard (indicato con la lettera greca sigma) è la seguente:
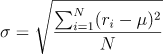
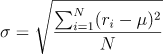
dove il rendimento μ è definito come la media dei rendimenti i-esimi della popolazione N:
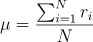
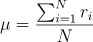
Calcolare la deviazione standard su Excel è molto semplice in quanto possiamo utilizzare la formula STDEV.P se stiamo operando sull’intera popolazione oppure STDEV.S se stiamo calcolando la deviazione standard per un campione (sample). Nella versione italiana le formule sono DEV.ST.P (popolazione) e DEV.ST.C (campione).
Esempio pratico: misurare il rischio di un portafoglio
Supponiamo di avere un portafoglio titoli con il seguente rendimento annuale:
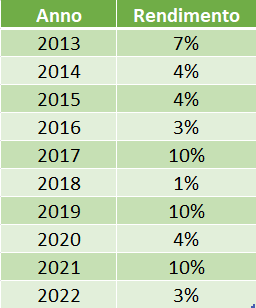

Per calcolare la deviazione standard il processo è il seguente:
- Calcoliamo la media dei rendimenti;
- Calcoliamo lo scarto tra la media dei rendimenti ed il singolo valore di rendimento;
- Eleviamo al quadrato i singoli scostamenti;
- Calcoliamo la varianza come somma tra gli scarti al quadrato diviso la numerica della popolazione;
- Calcoliamo la radice quadrata della varianza ed otteniamo lo scarto quadratico medio o deviazione standard. Avremmo raggiunto lo stesso risultato con la formula excel STDEV.P (per una popolazione) o STDEV.S (per un campione).


Cosa ci dice la deviazione standard? Ci dice che mediamente lo scarto rispetto alla media dei rendimenti negli ultimi 10 anni del nostro portafoglio è stata di ± 3.2. Come dato a se stante non è determinante per valutare la rischiosità assoluta di un portafoglio, in quanto non esiste una scala di valori ottimali per i quali una deviazione è traducibile in rischio basso, medio o alto, ma è utile come valore relativo e in particolar modo è utile in relazione al rendimento, in quanto a parità di rendimento l’investitore razionale tende ad orientarsi su portafogli che hanno una deviazione standard più bassa oppure a parità di deviazione standard si orienterà su portafogli che hanno un rendimento più alto.
Un chiave di lettura molto interessante che relaziona rendimento e deviazione standard è l’Indice di Sharpe.
💡 Vuoi semplificare la gestione del tuo portafoglio?
Con broker moderni come [Scalable Capital] hai accesso a:
✅ Analisi del rischio automatica del portafoglio
✅ Report sulla volatilità dei tuoi investimenti
✅ Strumenti di diversificazione guidata
✅ Dashboard con Indice di Sharpe calcolato
⚡ Apertura in 10 minuti • ✅ Nessun deposito minimo obbligatorio • 💳 PAC su ETF gratis
Link affiliato – Ricevo una commissione senza costi aggiuntivi per te. Info sulla trasparenza
Indice di Sharpe: misurare rendimento e rischio insieme
L’indice di Sharpe è un coefficiente che misura in modo assoluto le performance di un portafoglio, ossia ci consente di misurare il rischio di un investimento in relazione al suo rendimento. Viene anche definito come il rendimento ottenuto per ogni unità di rischio.
Mette in relazione il rendimento, al netto del rendimento risk-free, al rischio, inteso come volatilità ossia deviazione standard, di un portafoglio.
Il rendimento privo di rischio o risk-free rate è definito come l’interesse di una attività priva di rischio. Nella teoria nessuna attività è priva di rischio, tuttavia si assume che l’investimento in titoli di stato a breve termine di paesi tripla A sia un’attività risk-free, pertanto se il tasso di interesse di una obbligazione tripla A a breve termine è il 2%, significa che un investitore completamente razionale opterà sempre per l’investimento in titoli di stato se il rendimento di un investimento alternativo è minore o uguale al 2%, in quanto si preferisce investire in attività con minor rischio a parità di rendimento.
La differenza tra il rendimento di un investimento alternativo e il risk-free rate è definita come risk premium. Molto semplicemente, l’investitore viene “premiato” per essersi assunto un rischio maggiore ed il suo rendimento atteso aumenterà tanto più il rischio assunto è maggiore.
La formula di calcolo dell’indice di Sharpe è la seguente:
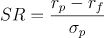
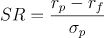
rp = rendimento del portafoglio
rf = risk-free rate
σp = deviazione standard del portafoglioIn linea di massima un investitore tenderà a preferire portafogli con Indice di Sharpe più alti, in quanto denotano un maggior rendimento a parità di rischio oppure un minor rischio a parità di rendimento.
Limiti del calcolo della volatilità (e alternative moderne 2025)
Un limite dell’indice di Sharpe è relativo al fatto che, mettendo in relazione rendimento e rischio, non fornisce un’indicazione in senso assoluto sui rendimenti e sulla volatilità del nostro portafoglio, ma lo fa fornendo un indicazione in senso assoluto come rapporto tra le due variabili.
Immaginiamo di avere un portafoglio A con rendimento atteso 5% e deviazione standard 10% ed un portafoglio B con rendimento atteso 20% e deviazione standard 40%. Assumiamo per semplicità un risk-free rate di 0.
L’indice di Sharpe sia del portafoglio A che del portafoglio B sarà 0.5 (0.05/0.1 nel primo caso e 0.2/0.4 nel secondo caso). Il portafoglio A tuttavia è un portafoglio meno volatile, ma sicuramente meno redditizio, mentre il portafoglio B è un portafoglio più rischioso ma che ha un rendimento molto più elevato.
Una soluzione a questo problema potrebbe essere di scegliere portafogli con Indice di Sharpe più alto a parità di volatilità.
Un secondo punto di attenzione riguarda il caso in cui il calcolo dell’Indice di Sharpe sia negativo. In questo caso l’investitore razionale tenderà sempre a minimizzare il rischio massimizzando il rendimento quindi in caso di Sharpe Ratio negativo, ci orienteremo sempre sull’acquisto di titoli di stato a breve termine tripla A.
Nassim Taleb, matematico, filosofo e trader di fama mondiale (se avete dato una letta al Cigno Nero lo sapete) è un fervente sostenitore del modello frattale applicato ai mercati finanziari, in quanto li identifica come facenti parte dell’Estremistan e sostiene che il calcolo della deviazione standard (quindi l’applicazione di modelli matematici basati sulla campana di Gauss) ai mercati è completamente sbagliata in quanto la gaussiana è applicabile unicamente al Mediocristan (la parte del mondo dove non esistono eventi estremi, come l’altezza o il peso medio della popolazione).
Senza addentrarci troppo nei tecnicismi, sappiate che applicando la gaussiana le probabilità che un evento si verifichi sono tanto più basse quanto più ci allontaniamo dalla media.
Le probabilità che un evento cada all’interno:
- di 1 deviazione standard dalla media è del 68.3%;
- di 2 deviazioni standard dalla media è del 95.4%;
- di 3 deviazioni standard dalla media è del 99.7%.


Consideriamo che un evento che ha uno scostamento dalla media di 6 deviazioni standard (6 sigma) è probabile che accada mediamente una volta ogni due milioni di anni.
Ribassi come quello del Black Monday del 1989 è un evento 20 sigma (o 25 sigma se non consideriamo i rendimenti del black monday nel calcolo dei rendimenti e della volatilità). Sarebbe come vincere una lotteria con una probabilità di 1 biglietto vincente su 2,5 milioni. E dovremmo farlo consecutivamente tra le 21 e le 22 volte (fonte: https://arxiv.org/pdf/1103.5672 ).
Domande frequenti sul rischio investimenti
Cos’è il rischio di un investimento?
Il rischio di un investimento è la possibilità che il rendimento effettivo differisca da quello atteso. Viene misurato principalmente attraverso la volatilità, calcolata
con la deviazione standard dei rendimenti storici.
Come si calcola il rischio di un portafoglio?
Il rischio di un portafoglio si calcola attraverso:
- Raccolta dei rendimenti storici
- Calcolo della deviazione standard con Excel (formula DEV.ST.P)
- Analisi dell’Indice di Sharpe per valutare il rapporto rischio/rendimento
Qual è un livello di rischio accettabile per un portafoglio?
Non esiste un valore assoluto ideale. A parità di rendimento, meglio scegliere portafogli con volatilità più bassa. L’Indice di Sharpe aiuta a confrontare portafogli diversi.
Come ridurre il rischio del portafoglio investimenti?
Per ridurre il rischio:
- Diversifica tra asset class diverse
- Bilancia azionario e obbligazionario
- Considera la correlazione tra gli asset
- Ribilancia periodicamente il portafoglio
🎯 Preferisci una gestione professionale del rischio?
Moneyfarm costruisce portafogli ottimizzati per il tuo profilo di rischio:
✅ Analisi professionale della tua tolleranza al rischio
✅ Portafoglio bilanciato automaticamente
✅ Monitoraggio continuo della volatilità
✅ Ribilanciamento automatico per mantenere il profilo di rischio target
⚡ Analisi in 10 minuti • 🤝 Consulente dedicato • 📊 Portafogli diversificati
Link di affiliazione. Non ci sono costi aggiuntivi – Info sulla trasparenza
Conclusioni: misurare il rischio nel 2025
Pur con i suoi limiti, la stima del rischio tramite deviazione standard è un metodo oggettivo e misurabile. Inoltre ha il vantaggio di non richiedere software matematici avanzati per il calcolo, ma sono sufficienti una serie storica di rendimenti ed excel.
Come per quanto riguarda il calcolo dei rendimenti, non è necessario perdere troppo tempo dietro a misurare il rischio di un investimento con perfetta precisione (storica), ma è utile periodicamente (per esempio annualmente, in fase di ribilanciamento) fare una valutazione di questo tipo e vedere come si sta muovendo il nostro portafoglio.
Grazie per la lettura.
Se questo articolo ti è stato utile, ecco alcuni modi per supportare il blog (e migliorare le tue finanze):
Strumenti che uso e consiglio
- Scalable Capital – Un broker che uso personalmente. Regime dichiarativo, oltre 2.500 ETF senza commissioni di acquisto, perfetto per PAC automatici.
- Moneyfarm – Gestione patrimoniale automatizzata con sostituto d’imposta. Ideale se non vuoi sbatterti a gestire tutto da solo senza farti mangiare dai costi delle banche tradizionali.
- Hype – Conto corrente a zero spese con IBAN italiano. Usa il codice HELLOHYPER per ottenere fino a 25€ di bonus all’apertura.
Risparmia sulle bollette
- Switcho – Servizio gratuito per trovare automaticamente il miglior fornitore di luce e gas. Il cambio è automatico e senza interruzioni.
Continua a imparare
- Audible – Ascolta i migliori libri di finanza durante i tragitti. Prova gratuita o 0,99€ per 3 mesi.
- Kindle Unlimited – Accesso illimitato a migliaia di ebook, molti gratuiti o scontati. Primo mese gratis.
Questi sono link affiliati. Se decidi di provare questi servizi, il blog riceve una piccola commissione senza alcun costo aggiuntivo per te. Consiglio solo strumenti che uso personalmente o che ritengo validi. Non sei obbligato a usarli, ma se l’hai trovato utile questo articolo, è un modo per supportare il progetto e permettermi di continuare a creare contenuti gratuiti.
Se ti è piaciuto l’articolo, iscriviti per rimanere aggiornato
Niente spam, ti invierò solo un aggiornamento settimanale.
DISCLAIMER
Non sono un consulente finanziario, ma un investitore comune che condivide il proprio percorso. Questo articolo è a scopo educativo. Le performance passate non garantiscono rendimenti futuri. La tassazione, i costi e le performance possono differire dai dati storici. Valuta attentamente la tua situazione personale, tolleranza al rischio e obiettivi finanziari. Se hai dubbi, consulta un professionista qualificato.